Using Logistic Regression in Research
Binary Logistic Regression is a statistical analysis that determines how much variance, if at all, is explained on a dichotomous dependent variable by a set of independent variables.
Questions Answered:
How does the probability of getting lung cancer change for every additional pound of overweight and for every X cigarettes smoked per day?
Do body weight calorie intake, fat intake, and age have an influence on heart attacks (yes vs. no)?

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
The major assumptions are:
- That the outcome must be discrete, otherwise explained as, the dependent variable should be dichotomous in nature (e.g., presence vs. absent);
- There should be no outliers in the data, which can be assessed by converting the continuous predictors to standardized, or z scores, and remove values below -3.29 or greater than 3.29.
- There should be no high intercorrelations (multicollinearity) among the predictors. This can be assessed by a correlation matrix among the predictors. Tabachnick and Fidell (2012) suggest that as long correlation coefficients among independent variables are less than 0.90 the assumption is met.
Categorical outcome variables with more than two categories can be handled using special forms of logistic regression. Outcome variables with three or more categories which are not ordered can be examined using multinomial logistic regression, while ordered outcome variables can be examined using various forms of ordinal logistic regression. These techniques require a number of additional assumptions and tests, so we will focus now strictly on binary logistic regression.
Binary logistic regression is estimated using Maximum Likelihood Estimation (MLE), unlike linear regression which uses the Ordinary Least Squares (OLS) approach. MLE is an iterative procedure, meaning that it starts with a guess as to the best weight for each predictor variable (that is, each coefficient in the model) and then adjusts these coefficients repeatedly until there is no additional improvement in the ability to predict the value of the outcome variable (either 0 or 1) for each case. While OLS regression can be visualized as the process of finding the line which best fits the data, logistic regression is more similar to crosstabulation given that the outcome is categorical and the test statistic utilized is the Chi Square
How is logistic regression run in SPSS and how is the output interpreted?
In SPSS, binary logistic regression is located on the Analyze drop list, under theRegression menu. The outcome variable – which must be coded as 0 and 1 – is placed in the first box labeled Dependent, while all predictors are entered into the Covariates box (categorical variables should be appropriately dummy coded). SPSS predicts the value labeled 1 by default, so careful attention should be paid to the coding of the outcome (usually it makes more sense to examine the presence of a characteristic or “success”).
SPSS produces lots of output for logistic regression, but below we focus on the most important panel of coefficients to determine the direction, magnitude, and significance of each predictor.
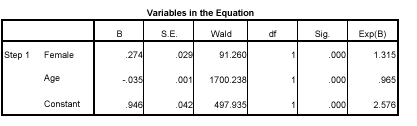
For example, let’s examine a study that is interested in whether or not individuals have been tested for HIV. Looking first at Age as a predictor, we see that the value in the column labeled B (also known as the logit, the logit coefficient, the logistic regression coefficient, or the parameter estimate) is -.035. This indicates that the association between age and testing is negative; that is, as age increases, testing for HIV decreases. Much like in OLS regression, a logit of 0 indicates no relationship while a positive logit is associated with an increase in the logged odds of success and a negative logit is associated with a decrease in the logged odds of success.
But what is the magnitude of this effect? Technically we could say that for every additional year of age, the odds of having been tested for HIV decrease by a factor of .035. This is not very intuitive, however, as we don’t generally have a strong sense of what odds are. In fact, it is much more common to look to the last column of this table, labeled Exp(B). This is the Odds Ratio and can be interpreted as the change in the odds of success. It is important to note that Odds Ratios (ORs) are relative to 1, meaning that an OR of 1 indicates no relationship while an OR greater than 1 indicates a positive relationship and an OR less than 1 a negative relationship. For most people ORs are most intuitively interpreted by converting to percent changes in the odds of success. This is simply done:
(Odds Ratio – 1) * 100 = percent change
So here we could say that each additional year of age reduces the odds of having been tested for HIV by 3.5%.
The interpretation of dummy-coded predictors is even easier in logistic regression. Here we compare the odds of those coded 1 (females in this example) to those coded 0 (males). Using the same simple equation as above, we find that women have 31.5% greater odds of having been tested for HIV compared to men. For both age and sex we see that the p-value is extremely small (< .01), so we conclude that each predictor is significantly associated with the outcome of interest.
What are special concerns with regard to logistic regression?
One key way in which logistic regression differs from OLS regression is with regard to explained variance or R2. Because logistic regression estimates the coefficients using MLE rather than OLS (see above), there is no direct corollary to explained variance in logistic regression. Nevertheless, many people want an equivalent way of describing how good a particular model is, and numerous pseudo-R2 values have been developed. These should be interpreted with extreme caution as they have many computational issues which cause them to be artificially high or low. A better approach is to present any of the goodness of fit tests available; Hosmer-Lemeshow is a commonly used measure of goodness of fit based on the Chi-square test (which makes sense given that logistic regression is related to crosstabulation).
.
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
- Edit your research questions and null/alternative hypotheses
- Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
- Justify your sample size/power analysis, provide references
- Explain your data analysis plan to you so you are comfortable and confident
- Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
- Clean and code dataset
- Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
- Conduct analyses to examine each of your research questions
- Write-up results
- Provide APA 6th edition tables and figures
- Explain chapter 4 findings
- Ongoing support for entire results chapter statistics
*Please call 877-437-8622 to request a quote based on the specifics of your research, or email [email protected].