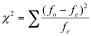Using Chi-Square Statistic in Research
Understanding the Chi-Square Test: A Simple Guide
What’s the Chi-Square Test For? The Chi-Square test checks if two categorical variables are related or just a coincidence.
Starting Point: The Null Hypothesis They’re independent. For example, it would assume that voter intent doesn’t depend on political party membership.
How Does It Work? Imagine a table (called a crosstabulation) showing how categories, like voter intent and political party, overlap. Each cell in the table shows the count of how many people or things fall into each combined category.
The Chi-Square test looks at the numbers in this table in two steps:
Expected vs. Observed: It first calculates the expected counts in each cell, assuming no relationship between the variables. Then, it compares these expected counts to the actual counts (observed) in your data.
The Chi-Square Statistic: Using these comparisons, it calculates a number (the Chi-Square statistic). If the number is large enough, it indicates the observed counts differ too much from the expected counts to be a coincidence. This means there’s likely a significant relationship between the variables.
Example Question
“Is there a significant relationship between voter intent and political party membership?”
Using the Chi-Square test, we can analyze data from surveys or polls to see if voter intent really varies by political party, or if any patterns we see could just be random.
Key Takeaways
The Chi-Square test is a handy tool for exploring relationships between categorical variables. It compares what we observe to what we’d expect. Also, it helps us determine if the variables are independent or if there’s a relationship.
The calculation of this statistic is quite straight-forward and intuitive:
where fo = the observed frequency (the observed counts in the cells)
and fe = the expected frequency if NO relationship existed between the variables
As depicted in the formula, the Chi-Square statistic compares the difference between what the data actually show and what we would expect if there were truly no relationship between the variables.
How is the Chi-Square statistic run in SPSS and how is the output interpreted?
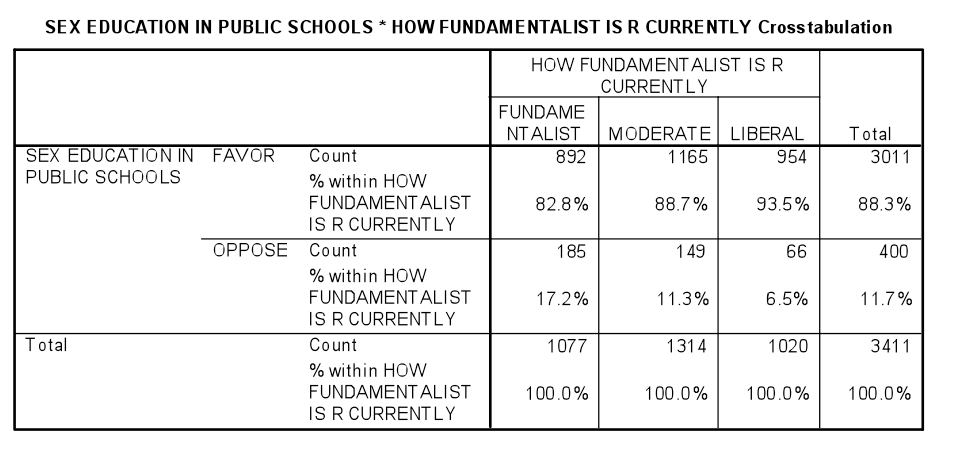
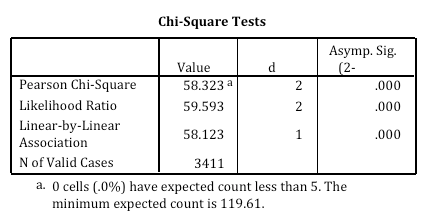
The Chi-Square statistic appears as an option when requesting a crosstabulation in SPSS. The software labels the output as Chi-Square Tests, and it labels the Chi-Square statistic used in the Test of Independence as Pearson Chi-Square. Researchers calculate the degrees of freedom as the number of rows – 1 multiplied by the number of columns – 1, and they evaluate this statistic by comparing the actual value against a critical value found in a Chi-Square distribution. However, they often find it easier to simply examine the p-value provided by SPSS. To make a conclusion about the hypothesis with 95% confidence, the value labeled Asymp. Sig. (which is the p-value of the Chi-Square statistic) should be less than .05 (which is the alpha level associated with a 95% confidence level).
Is the p-value (labeled Asymp. Sig.) less than .05? If so, we can conclude that the variables are not independent of each other and that there is a statistical relationship between the categorical variables.
In this example, there is an association between fundamentalism and views on teaching sex education in public schools. While 17.2% of fundamentalists oppose teaching sex education, only 6.5% of liberals are opposed. The p-value shows that the variables are not independent and that a statistically significant relationship exists between them.
What are special concerns with regard to the Chi-Square statistic?
There are a number of important considerations when using this statistic to evaluate a crosstabulation. The calculation of it’s value makes it extremely sensitive to sample size – when the sample size is too large (~500), almost any small difference appears statistically significant. It is also sensitive to the distribution within the cells, and SPSS gives a warning message if cells have fewer than 5 cases. You can address this by using categorical variables with a limited number of categories, such as by combining categories if necessary to produce a smaller table.
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
Please call 727-442-4290 to request a quote based on the specifics of your research, schedule a consultation here, or email [email protected]