The Multiple Linear Regression Analysis in SPSS
This example is based on the FBI’s 2006 crime statistics. Particularly we are interested in the relationship between size of the state, various property crime rates and the number of murders in the city. It is our hypothesis that less violent crimes open the door to violent crimes. We also hypothesize that even we account for some effect of the city size by comparing crime rates per 100,000 inhabitants that there still is an effect left.
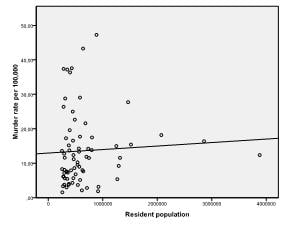
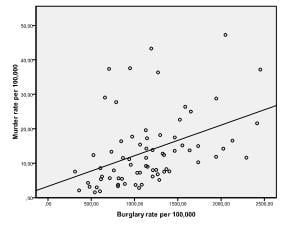
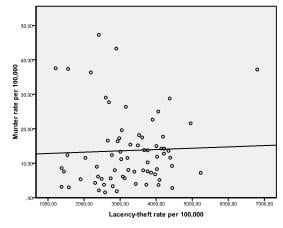
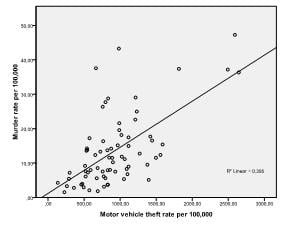
First we need to check whether there is a linear relationship between the independent variables and the dependent variable in our multiple linear regression model. To do this, we can check scatter plots. The scatter plots below indicate a good linear relationship between murder rate and burglary and motor vehicle theft rates, and only weak relationships between population and larceny.
Regression help?
Option 1: User-friendly Software
Transform raw data to written interpreted results in seconds.
Option 2: Professional Statistician
Collaborate with a statistician to complete and understand your results.
Secondly, we need to check for multivariate normality. We can do this by checking normal Q-Q plots of each variable. In our example, we find that multivariate normality might not be present in the population data (which is not surprising since we truncated variability by selecting the 70 biggest cities).
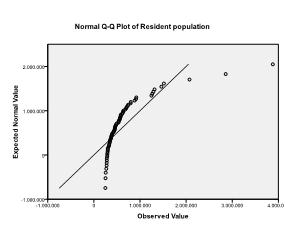
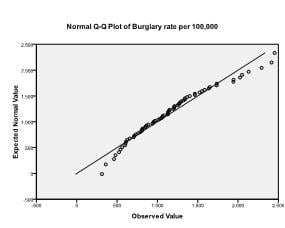
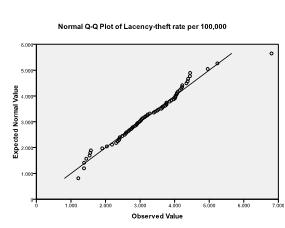
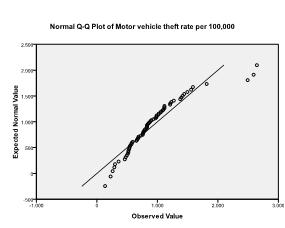
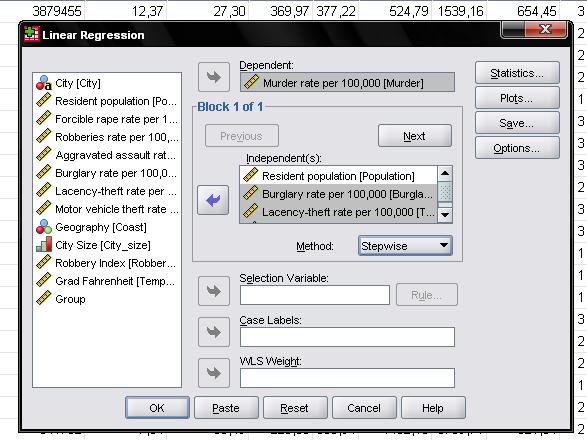
We will ignore this violation of the assumption for now, and conduct the multiple linear regression analysis. Multiple linear regression is found in SPSS in Analyze/Regression/Linear…
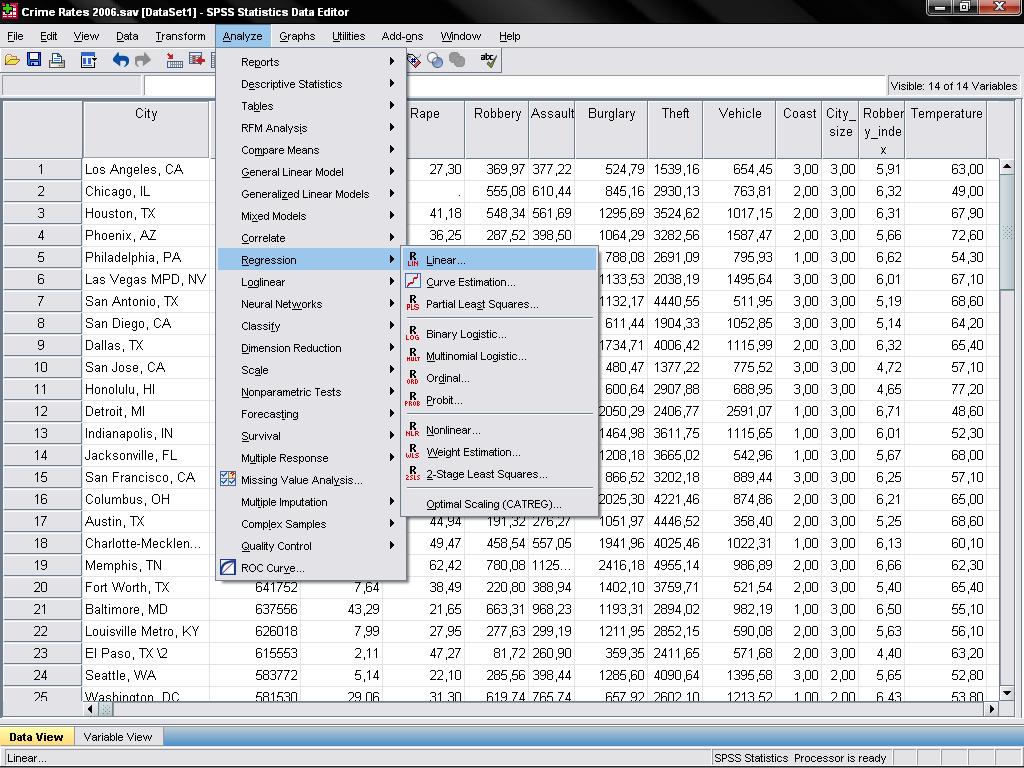
In our example, we need to enter the variable “murder rate” as the dependent variable and the population, burglary, larceny, and vehicle theft variables as independent variables. In this case, we will select stepwise as the method. The default method for the multiple linear regression analysis is ‘Enter’. That means that all variables are forced to be in the model. However, since over fitting is a concern of ours, we want only the variables in the model that explain a significant amount of additional variance.
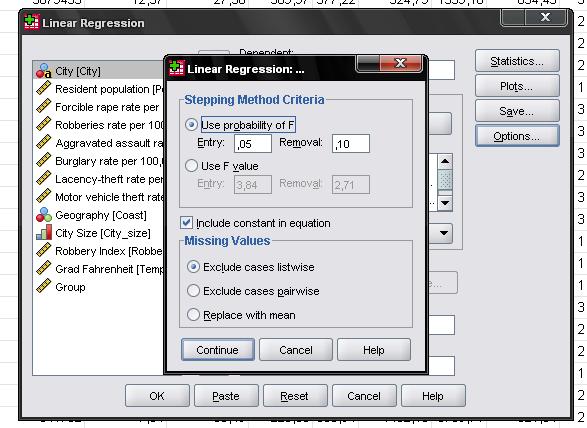
In the field “Options…” we can set the stepwise criteria. We want to include variables in our multiple linear regression model that increase the probability of F by at least 0.05 and we want to exclude them if the increase F by less than 0.1.
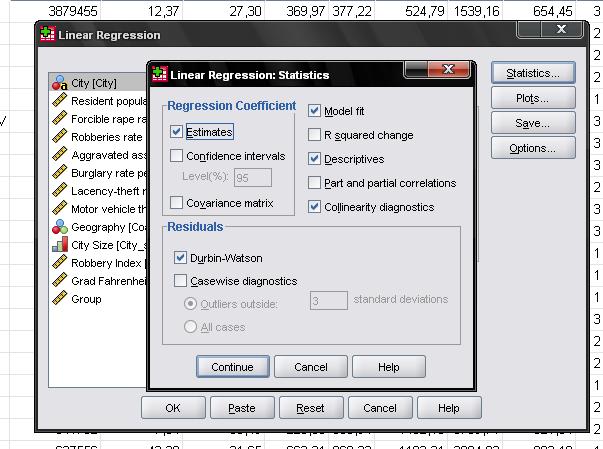
The “Statistics…” menu allows us to include additional statistics that we need to assess the validity of our linear regression analysis.
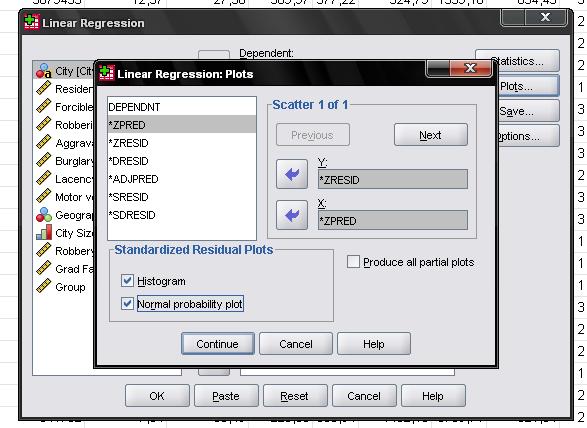
It is advisable to include the collinearity diagnostics and the Durbin-Watson test for auto-correlation. To test the assumption of homoscedasticity and normality of residuals we will also include a special plot from the “Plots…” menu.
The first table in the results output tells us the variables in our analysis. Turns out that only motor vehicle theft is useful to predict the murder rate.
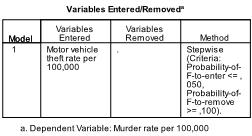
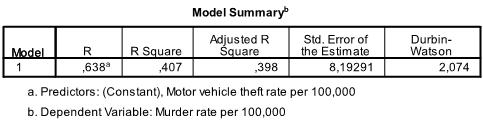
The next table shows the multiple linear regression model summary and overall fit statistics. We find that the adjusted R² of our model is .398 with the R² = .407. This means that the linear regression explains 40.7% of the variance in the data. The Durbin-Watson d = 2.074, which is between the two critical values of 1.5 < d < 2.5. Therefore, we can assume that there is no first order linear auto-correlation in our multiple linear regression data.
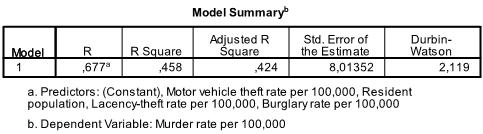
If we would have forced all variables (Method: Enter) into the linear regression model, we would have seen a slightly higher R² and adjusted R² (.458 and .424 respectively).
The next output table is the F-test. The linear regression’s F-test has the null hypothesis that the model explains zero variance in the dependent variable (in other words R² = 0). The F-test is highly significant, thus we can assume that the model explains a significant amount of the variance in murder rate.
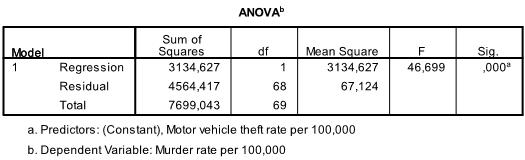
The next table shows the multiple linear regression estimates including the intercept and the significance levels.
In our stepwise multiple linear regression analysis, we find a non-significant intercept but highly significant vehicle theft coefficient, which we can interpret as: for every 1-unit increase in vehicle thefts per 100,000 inhabitants, we will see .014 additional murders per 100,000.
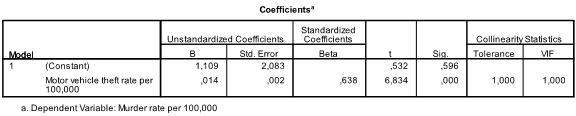
If we force all variables into the multiple linear regression, we find that only burglary and motor vehicle theft are significant predictors. We can also see that motor vehicle theft has a higher impact than burglary by comparing the standardized coefficients (beta = .507 versus beta = .333).
The information in the table above also allows us to check for multicollinearity in our multiple linear regression model. Tolerance should be > 0.1 (or VIF < 10) for all variables, which they are.
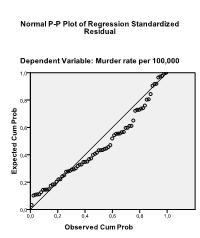
Lastly, we can check for normality of residuals with a normal P-P plot. The plot shows that the points generally follow the normal (diagonal) line with no strong deviations. This indicates that the residuals are normally distributed.
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
Edit your research questions and null/alternative hypotheses
Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
Justify your sample size/power analysis, provide references
Explain your data analysis plan to you so you are comfortable and confident
Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
Clean and code dataset
Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
Conduct analyses to examine each of your research questions
Write-up results
Provide APA 7th edition tables and figures
Explain Chapter 4 findings
Ongoing support for entire results chapter statistics
Please call 727-442-4290 to request a quote based on the specifics of your research, schedule using the calendar on this page, or email [email protected]