Conduct and Interpret a One-Way ANOVA
What is the One-Way ANOVA?
One-Way ANOVA, standing for Analysis Of Variance, is a statistical method used to determine if there are significant differences between the averages of two or more unrelated groups. This technique is particularly useful when you want to compare the effect of one single factor (independent variable) across different groups on a specific outcome (dependent variable).
Beyond Basic Comparison
While ANOVA is primarily used to compare differences, it often goes a step further by exploring cause-and-effect relationships. It suggests that the differences observed among groups are due to one or more controlled factors. Essentially, these factors categorize the data points into groups, leading to variations in the average outcomes of these groups.
Example Simplified
Imagine we’re curious about whether there’s a difference in hair length between genders. We gather a group of twenty undergraduate students, half identified as female and half as male, and measure their hair length.
- Conservative Approach: A cautious statistician might say, “After measuring the hair length of ten female and ten male students, our analysis shows that, on average, female students have significantly longer hair than male students.”
- Assertive Approach: A more assertive statistician might interpret the results to mean that gender directly influences hair length, suggesting a cause-and-effect relationship.
Understanding ANOVA’s Role
Most statisticians lean towards the assertive approach, viewing ANOVA as a tool for analyzing dependencies. This perspective sees ANOVA as not just comparing averages but testing the influence of one or more factors on an outcome. In statistical language, it’s about examining how independent variables (like gender in our example) affect dependent variables (such as hair length), assuming a functional relationship (Y = f(x1, x2, x3, … xn)).
In essence, One-Way ANOVA is a powerful method for not only identifying significant differences between groups but also for hinting at potential underlying causes for these differences. It’s a foundational tool in the statistical analysis of data, enabling researchers to draw meaningful conclusions about the effects of various factors on specific outcomes.
ANOVA help?
Option 1: User-friendly Software
Transform raw data to written interpreted results in seconds.
Option 2: Professional Statistician
Collaborate with a statistician to complete and understand your results.
The ANOVA is a popular test; it is the test to use when conducting experiments. This is due to the fact that it only requires a nominal scale for the independent variables – other multivariate tests (e.g., regression analysis) require a continuous-level scale. This following table shows the required scales for some selected tests.
| Independent Variable | |||
| Metric | Non-metric | ||
| DependentVariable | metric | Regression | ANOVA |
| Non-metric | Discriminant Analysis | χ² (Chi-Square) |
The F-test, the T-test, and the MANOVA are all similar to the ANOVA. The F-test is another name for an ANOVA that only compares the statistical means in two groups. This happens if the independent variable for the ANOVA has only two factor steps, for example male or female as a gender.
The T-test compares the means of two (and only two) groups when the variances are not equal. The equality of variances (also called homoscedasticity or homogeneity) is one of the main assumptions of the ANOVA (see assumptions, Levene Test, Bartlett Test). MANOVA stands for Multivariate Analysis of Variance. Whereas the ANOVA can have one or more independent variables, it always has only one dependent variable. On the other hand the MANOVA can have two or more dependent variables.
Examples for typical questions the ANOVA answers are as follows:
- Medicine – Does a drug work? Does the average life expectancy significantly differ between the three groups that received the drug versus the established product versus the control?
- Sociology – Are rich people happier? Do different income classes report a significantly different satisfaction with life?
- Management Studies – What makes a company more profitable? A one, three or five-year strategy cycle?
The One-Way ANOVA in SPSS
Let’s consider our research question from the Education studies example. Do the standardized math test scores differ between students that passed the exam and students that failed the final exam? This question indicates that our independent variable is the exam result (fail vs. pass) and our dependent variable is the score from the math test. We must now check the assumptions.
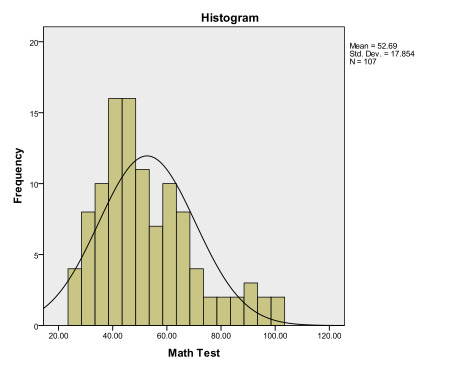
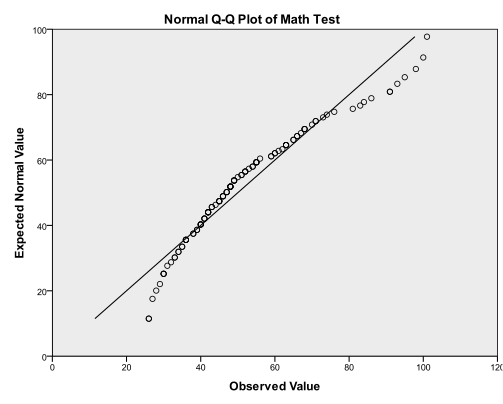
First we examine the multivariate normality of the dependent variable. We can check graphically either with a histogram (Analyze/Descriptive Statistics/Frequencies… and then in the menu Charts…) or with a Q-Q-Plot (Analyze/Descriptive Statistics/Q-Q-Plot…). Both plots show a somewhat normal distribution, with a skew around the mean.
Secondly, we can test for multivariate normality with the Kolmogorov-Smirnov goodness of fit test (Analyze/Nonparacontinuous-level Test/Legacy Dialogs/1 Sample K S…). An alternative to the K-S test is the Chi-Square goodness of fit test, but the K-S test is more robust for continuous-level variables.
The K-S test is not significant (p = 0.075) thus we cannot reject the null hypothesis that the sample distribution is multivariate normal. The K-S test is one of the few tests where a non-significant result (p > 0.05) is the desired outcome.
If normality is not present, we could exclude the outliers to fix the problem, center the variable by deducting the mean, or apply a non-linear transformation to the variable creating an index.
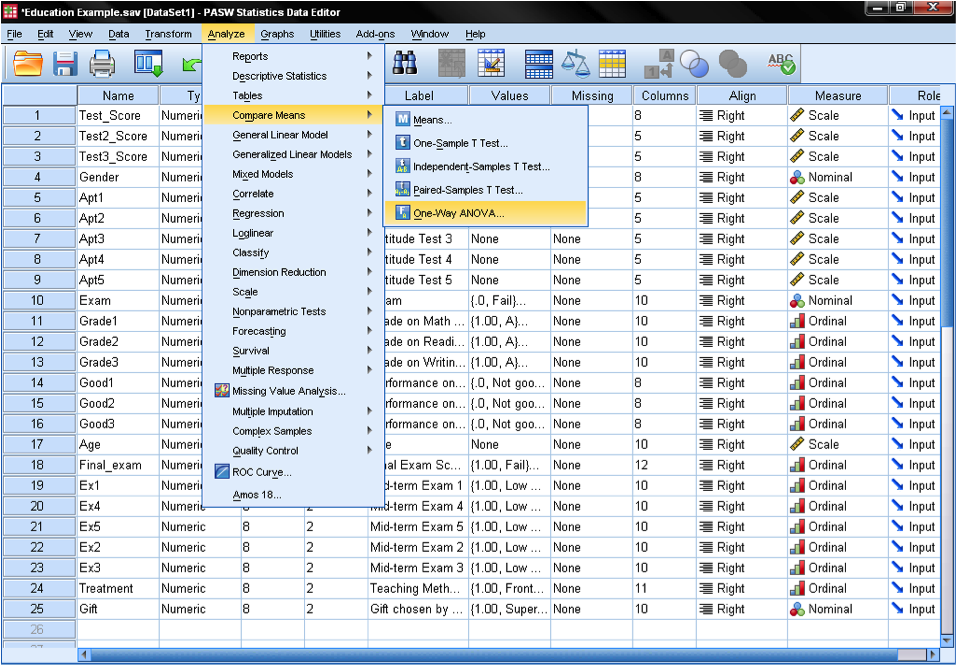
The ANOVA can be found in SPSS in Analyze/Compare Means/One Way ANOVA.
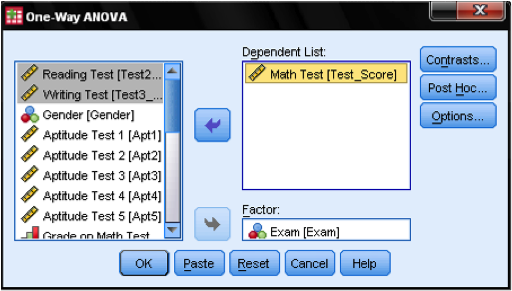
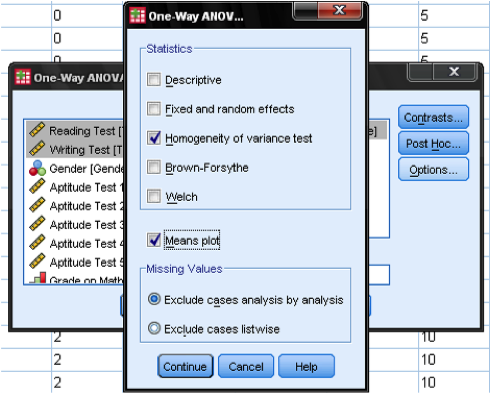
In the ANOVA dialog we need to specify our model. As described in the research question we want to test, the math test score is our dependent variable and the exam result is our independent variable. This would be enough for a basic analysis. But the dialog box has a couple more options around Contrasts, post hoc tests (also called multiple comparisons), and Options.
In the dialog box options we can specify additional statistics. If you find it useful you might include standard descriptive statistics. Generally you should select the Homogeneity of variance test (which is the Levene test of homoscedasticity), because as we find in our decision tree the outcome of this test is the criterion that decides between the t-test and the ANOVA.
Options
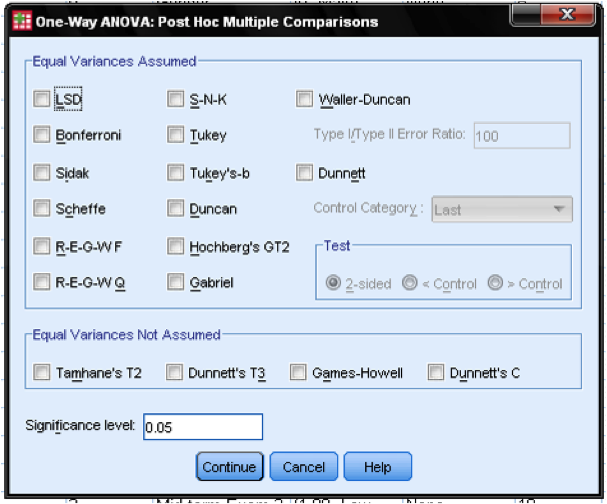
Post Hoc Tests
Post Hoc tests are useful if your independent variable includes more than two groups. In our example the independent variable just specifies the outcome of the final exam on two factor levels – pass or fail. If more than two factor levels are given it might be useful to run pairwise tests to test which differences between groups are significant. Because executing several pairwise tests in one analysis decreases the degrees of freedom, the Bonferoni adjustment should be selected, which corrects for multiple pairwise comparisons. Another test method commonly employed is the Student-Newman-Keuls test (or short S-N-K), which pools the groups that do not differ significantly from each other. Therefore this improves the reliability of the post hoc comparison because it increases the sample size used in the comparison.
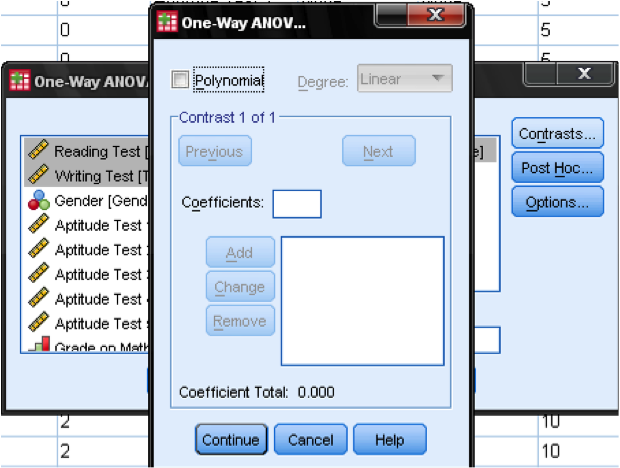
Contrasts
The last dialog box is contrasts. Contrasts are differences in mean scores. It allows you to group multiple groups into one and test the average mean of the two groups against our third group. Please note that the contrast is not always the mean of the pooled groups! Contrast = (mean first group + mean second group)/2. It is only equal to the pooled mean, if the groups are of equal size. It is also possible to specify weights for the contrasts, e.g., 0.7 for group 1 and 0.3 for group 2. We do not specify contrasts for this demonstration.
Need More Help?
Check out our online course for conducting an ANOVA here.
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
Edit your research questions and null/alternative hypotheses
Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
Justify your sample size/power analysis, provide references
Explain your data analysis plan to you so you are comfortable and confident
Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
Clean and code dataset
Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
Conduct analyses to examine each of your research questions
Write-up results
Provide APA 7th edition tables and figures
Explain Chapter 4 findings
Ongoing support for entire results chapter statistics
Please call 727-442-4290 to request a quote based on the specifics of your research, schedule using the calendar on this page, or email [email protected]