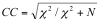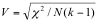Nominal Variable Association
Nominal variable association refers to the statistical relationship(s) on nominal variables. Nominal variables are variables that are measured at the nominal level, and have no inherent ranking. Examples of nominal variables that are commonly assessed in social science studies include gender, race, religious affiliation, and college major. Crosstabulation (also known as contingency or bivariate tables) is commonly used to examine the relationship between nominal variables Chi Square tests-of-independence are widely used to assess relationships between two independent nominal variables.
Questions answered:
Does a relationship exist between graduation intent and gender?
Is there an association between music genre selection and venue type?

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
Crosstabulation shows whether being in one category of the independent variable makes a case more likely to be in a particular category of the dependent variable. This allows researchers to examine the association between two categorical variables. . Using the variables above as an example, crosstabulation can address the association between race and college major: are African American students more likely to major in business or are Hispanic students more likely to major in the natural sciences. Patterns of association can be examined simply by comparing the observed frequencies across rows of the table (assuming that the convention of putting the independent variable in the columns and the dependent variable in the rows has been followed) and comparing it to the calculated expected frequencies. Using a Chi-Square Test of Independence allows researchers to assess whether the relationship observed between the nominal variables in a particular sample is also likely to be found in the population. However, this test may not be appropriate if the sample size is not sufficient.
Several measures also exist which allow researchers to evaluate the strength of the association between two nominal variables. Such measures are similar to Pearson’s correlation in that that they have specific bounds within which they fall and therefore provide a standard way of speaking about the strength of the association between two nominal variables.
Each of the following measures uses the Chi-Square value calculated for the crosstabulation table of interest. The contingency coefficient is calculated as follows:
This measure ranges between 0 and 1, with values closer to 1 indicating a stronger association between the variables. The CC is highly sensitive to the size of the table and should therefore be interpreted with caution.
A general rule of thumb for interpreting the strength of associations is:
< .10 = weak
.11 – .30 = moderate
> .31 = strong
Contingency Coefficient
Phi Coefficient
A measure of association used for 2 x 2 tables is the Phi coefficient:
Again, the measure ranges between 0 and 1 with higher values meaning a stronger association.
Cramer’s V
When the crosstabulation table is larger than 2 x 2, Cramer’s V is the best choice:
Here, N is the sample size and k is the smaller of the number of rows or columns (so it would be 3 for a 3 x 4 table).
Lambda
Unlike the above Chi-Square based measures, Lambda is a Proportional Reduction in Error (PRE) measure which is interpreted as the amount of variance accounted for in predicting the dependent variable that can be attributed by the independent variable. Another way to say this is: how much better is our guess about which category of the dependent variable each case will fall into if we know the case’s value on the independent variable? Much like R-squared in regression (which is also a PRE measure), lambda is often represented as a percentage. Lambda is a directional measure in that the calculation differs based on which variable is treated as the independent variable.
All of the above measures of association are available by clicking on the Statistics button when requesting crosstabulations in SPSS. Lambda is calculated in both directions, treating each variable as independent. The other three measures are symmetric, meaning that it does not matter which variable is treated as independent
Assumptions:
Adequate sample size for each of the categories being analyzed.
Variables must be categorical.
If a zero is present in the crosstabulation, no association can be assessed.
Related analyses: