When does selection of indicator variable constraints matter in CFA and SEM?
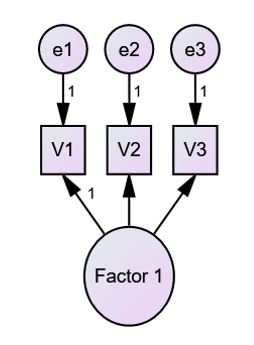
Confirmatory factor analysis (CFA) is an advanced statistical technique used to determine how well a set of observed variables (i.e., indicators) are represented by one or more pre-determined latent factors. Structural equation modeling (SEM) is an extension of CFA wherein specific theorized relationships among the latent factors are tested. In both types of analyses, each latent variable is represented by multiple indicators. For example, in the diagram below, the latent factor (Factor 1) is represented by three observed indicators (V1, V2, and V3).

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
To ensure that the CFA or SEM is identified, a constraint is typically added to one of the indicators for each latent variable. In the example above, the constraint is set on V1, as indicated by the “1” on the path arrow leading from Factor 1 to V1. This means that the unstandardized path from the latent factor to the indicator is fixed to 1. By doing this, we are essentially specifying a reference point from which the rest of the indicators (which would be V2 and V3 in this example) can be estimated in terms of their relation to the latent factor.
Now, you may ask why we decided to constrain V1, as opposed to V2 or V3. Does it matter which indicator we decide to constrain? In many cases, it does not matter which indicator you choose. In fact, CFA/SEM statistical software often will automatically select this for you (e.g., pick the first indicator in the list). Assuming all of your indicators are strong, valid measures of the overall construct, any one of them can serve as your reference point. However, if you have a “bad” indicator present in your data, constraining that indicator may cause problems (i.e., invalid results or other error messages from your statistical software).
So, what is a “bad” indicator? A bad indicator is one that is either negatively or extremely weakly related to the other indicators. Negative or weak correlations are indicative of an indicator that needs to be reverse-coded or removed from the model entirely. If you run into problems with your model, you can check for bad indicators by looking at the standardized loadings (i.e., regression weights) for the indicators or bivariate correlations between the indicators. Look specifically at the indictor you have constrained; if the standardized loading is negative or weak (< 0.5), you should constrain a different indicator and consider recoding or removing the bad indicator.
In short, your choice of constraints can matter if you have indicators in your model that are negatively or weakly related to the other indicators of the same latent factor. You should avoid constraining these “bad” indicators to help ensure you get valid results.
