Conduct and Interpret a Canonical Correlation
What is Canonical Correlation analysis?
The Canonical Correlation is a multivariate analysis of correlation. Canonical is the statistical term for analyzing latent variables (which are not directly observed) that represent multiple variables (which are directly observed). The term can also be found in canonical regression analysis and in multivariate discriminant analysis.
Canonical Correlation analysis is the analysis of multiple-X multiple-Y correlation. The Canonical Correlation Coefficient measures the strength of association between two Canonical Variates.
A Canonical Variate is the weighted sum of the variables in the analysis. The canonical variate is denoted CV. Similarly to the discussions on why to use factor analysis instead of creating unweighted indices as independent variables in regression analysis, canonical correlation analysis is preferable in analyzing the strength of association between two constructs. This is such because it creates an internal structure, for example, a different importance of single item scores that make up the overall score (as found in satisfaction measurements and aptitude testing).

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
For multiple x and y the canonical correlation analysis constructs two variates CVX1 = a1x1 + a2x2 + a3x3 + … + anxn and CVY1 = b1y1 + b2y2 + b3y3 + … + bmym. The canonical weights a1…an and b1…bn are chosen so that they maximize the correlation between the canonical variates CVX1 and CVY1. A pair of canonical variates is called a canonical root. This step is repeated for the residuals to generate additional duplets of canonical variates until the cut-off value = min(n,m) is reached; for example, if we calculate the canonical correlation between three variables for test scores and five variables for aptitude testing, we would extract three pairs of canonical variates or three canonical roots. Note that this is a major difference from factor analysis. In factor analysis the factors are calculated to maximize between-group variance while minimizing in-group variance. They are factors because they group the underlying variables.
Canonical Variants are not factors because only the first pair of canonical variants groups the variables in such way that the correlation between them is maximized. The second pair is constructed out of the residuals of the first pair in order to maximize correlation between them. Therefore the canonical variants cannot be interpreted in the same way as factors in factor analysis. Also the calculated canonical variates are automatically orthogonal, i.e., they are independent from each other.
Similar to factor analysis, the central results of canonical correlation analysis are the canonical correlations, the canonical factor loadings, and the canonical weights. They can also be used to calculate d, the measure of redundancy. The redundancy measurement is important in questionnaire design and scale development. It can answer questions such as, “When I measure a five item satisfaction with the last purchase and a three item satisfaction with the after sales support, can I exclude one of the two scales for the sake of shortening my questionnaire?” Statistically it represents the proportion of variance of one set of variables explained by the variant of the other set of variables.
The canonical correlation coefficients test for the existence of overall relationships between two sets of variables, and redundancy measures the magnitude of relationships. Lastly Wilk’s lambda (also called U value) and Bartlett’s V are used as a Test of Significance of the canonical correlation coefficient. Typically Wilk’s lambda is used to test the significance of the first canonical correlation coefficient and Bartlett’s V is used to test the significance of all canonical correlation coefficients.
A final remark: Please note that the Discriminant Analysis is a special case of the canonical correlation analysis. Every nominal variable with n different factor steps can be replaced by n-1 dichotomous variables. The Discriminant Analysis is then nothing but a canonical correlation analysis of a set of binary variables with a set of continuous-level (ratio or interval) variables.
Canonical Correlation Analysis in SPSS
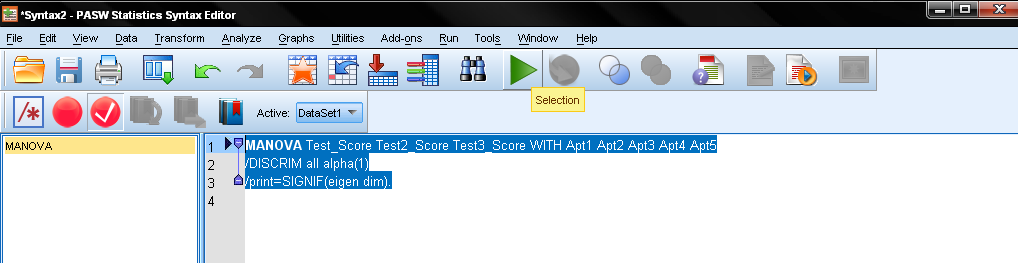
We want to show the strength of association between the five aptitude tests and the three tests on math, reading, and writing. Unfortunately, SPSS does not have a menu for canonical correlation analysis. So we need to run a couple of syntax commands. Do not worry—this sounds more complicated than it really is. First, we need to open the syntax window. Click on File/New/Syntax.
In the SPSS syntax we need to use the command for MANOVA and the subcommand /discrim in a one factorial design. We need to include all independent variables in one single factor separating the two groups by the WITH command. The list of variables in the MANOVA command contains the dependent variables first, followed by the independent variables (Please do not use the command BY instead of WITH because that would cause the factors to be separated as in a MANOVA analysis).
The subcommand /discrim produces a canonical correlation analysis for all covariates. Covariates are specified after the keyword WITH. ALPHA specifies the significance level required before a canonical variable is extracted, default is 0.25; it is typically set to 1.0 so that all discriminant functions are reported. Your syntax should look like this:
To execute the syntax, just highlight the code you just wrote and click on the big green Play button.
The Output of the Canonical Correlation Analysis
The syntax creates an overwhelmingly large output. No worries, we discuss the important bits of it next. The output starts with a sample description and then shows the general fit of the model reporting Pillai’s, Helling’s, Wilk’s and Roy’s multivariate criteria. The commonly used test is Wilk’s lambda, but we find that all of these tests are significant with p<.05.

The next section reports the canonical correlation coefficients and the eigenvalues of the canonical roots. The first canonical correlation coefficients and the eigenvalues of the canonical roots. The first canonical correlation coefficient is .81108 with an explained variance of the correlation of 96.87% and an eigenvalue of 1.92265. Thus indicating that our hypothesis is correct – generally the standardized test scores and the aptitude test scores are positively correlated.
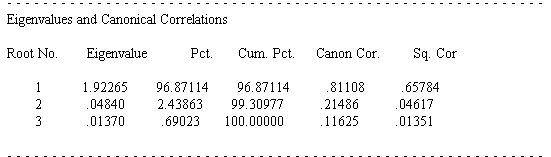
So far the output only showed overall model fit. The next part tests the significance of each of the roots. We find that of the three possible roots only the first root is significant with p < .05. Since our model contains the three test scores (math, reading, writing) and five aptitude tests, SPSS extracts three canonical roots or dimensions. The first test of significance tests all three canonical roots of significance (f = 9.26 p < .05), the second test excludes the first root and tests roots two to three, the last test tests root three by itself. In our example only the first root is significant p < .05.

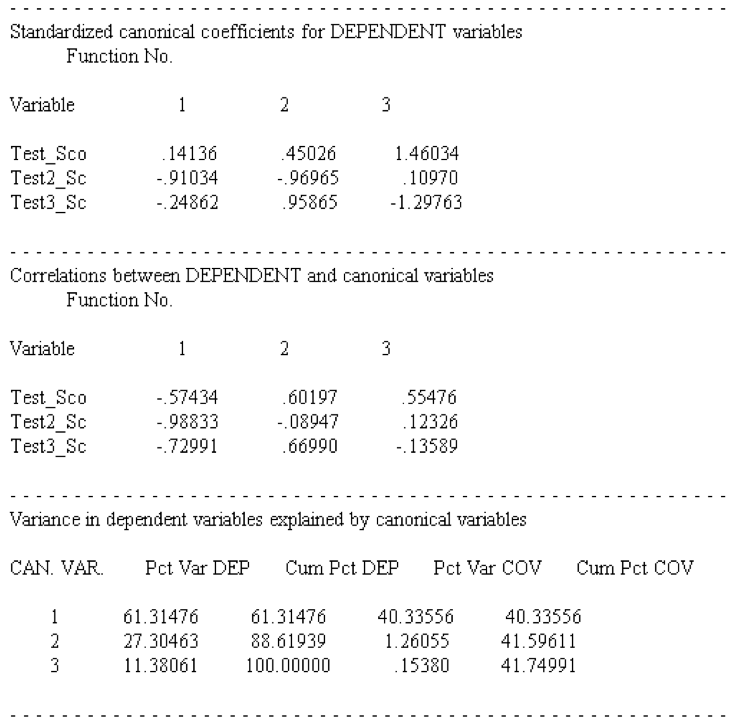
In the next parts of the output SPSS presents the results separately for each of the two sets of variables. Within each set, SPSS gives the raw canonical coefficients, standardized coefficients, correlations between observed variables, the canonical variant, and the percent of variance explained by the canonical variant. Below are the results for the 3 Test variables.

The raw canonical coefficients are similar to the coefficients in linear regression; they can be used to calculate the canonical scores.

Easier to interpret are the standardized coefficients (mean = 0, st.dev. = 1). Only the first root is relevant since root two and three are not significant. The strongest influence on the first root is variable Test_Score (which represents the math score).
The next section shows the same information (raw canonical coefficients, standardized coefficients, correlations between observed variables and the canonical variant, and the percent of variance explained by the canonical variant) for the aptitude test variables.