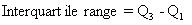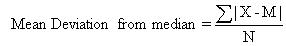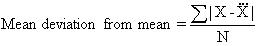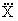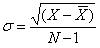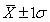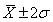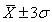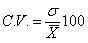Dispersion
In statistics, the measure of central tendency gives a single value that represents the whole value; however, the central tendency cannot describe the observation fully. The measure of dispersion helps us to study the variability of the items. In a statistical sense, dispersion has two meanings: first it measures the variation of the items among themselves, and second, it measures the variation around the average. If the difference between the value and average is high, then dispersion will be high. Otherwise it will be low. According to Dr. Bowley, “dispersion is the measure of the variation between items.” Researchers use this technique because it determines the reliability of the average. Dispersion also helps a researcher in comparing two or more series. It is also the facilitating technique to many other statistical techniques like correlation, regression, structural equation modeling, etc. In statistics, dispersion has two measure types. The first is the absolute measure, which measures the dispersion in the same statistical unit. The second type is the relative measure of dispersion, which measures the ratio unit. In statistics, there are many techniques that are applied to measure dispersion.Range: Range is the simple measure of dispersion, which is defined as the difference between the largest value and the smallest value. Mathematically, the absolute and the relative measure of range can be written as the following:
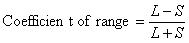
Quartile deviation: This is a measure of dispersion. In this method, the difference between the upper quartile and lower quartile is taken and is called the interquartile range. Symbolically it is as follows:
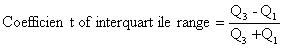
Mean Deviation: Mean deviation is a measure of dispersion, which is known as the average deviation. Mean deviation can be computed from the mean or median. Mean deviation is the arithmetic deviation of different items of central tendency. It may be the mean or the median. Symbolically, mean deviation is defined as the following:
= meanStandard Deviation: In the measure of dispersion, the standard deviation method is the most widely used method. In 1983, it was first used by Karl Pearson. Standard deviation is also known as root mean square deviation. Symbolically it is as follows:
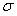
Variance= (S.D)
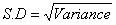
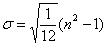
2. The sum of the square deviation taken by the arithmetical mean is minimal.3. In asymmetrical distribution, Standard deviation has the following relationship with the mean
, Including 68.27% of the items
Include the 99.73% of the items.Coefficient of variation: Coefficient of variation is the relative measure of the dispersion. This method was developed by Karl Pearson. Coefficient of variation is used, while measuring the dispersion of two series. Coefficient of variation can be calculated by using the following formula:

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.

We work with graduate students every day and know what it takes to get your research approved.
- Address committee feedback
- Roadmap to completion
- Understand your needs and timeframe