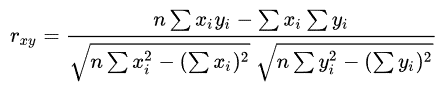Correlation (Pearson, Kendall, Spearman)
In summary, Correlation is a bivariate analysis that measures the strength of association between two variables and the direction of the relationship. Specifically, in terms of the strength of relationship, the value of the correlation coefficient varies between +1 and -1. For instance, a value of ± 1 indicates a perfect degree of association between the two variables. On the other hand, as the correlation coefficient value goes towards 0, the relationship between the two variables will be weaker. Additionally, the sign of the coefficient indicates direction of the relationship a + sign indicates a positive relationship and a – sign indicates a negative relationship.
Types of correlation:
Generally, in statistics, we measure four types of correlations: Pearson correlation, Kendall rank correlation, Spearman correlation, and the Point-Biserial correlation. The following software tools simplify the process of conducting a correlation analysis:
Available Courses:
Pearson r correlation:
Firstly, Pearson r correlation is the most commonly used statistic to measure the degree of the relationship between linearly related variables. For example, in the stock market, analyst use Pearson r correlation to measure the degree of relationship between the two. On the other hand, researchers apply the point-biserial correlation using the Pearson correlation formula when one of the variables is dichotomous. The following formula calculates the Pearson r correlation:
rxy = Pearson r correlation coefficient between x and y
n = number of observations
xi = value of x (for ith observation)
yi = value of y (for ith observation)
Types of research questions a Pearson correlation can examine:
Does age (measured in years) significantly relate to height (measured in inches)? That is to say, does it influence age?
Is there a relationship between temperature, measured in degrees Fahrenheit, and ice cream sales, measured by income? In other words, does temperature impact ice cream sales?
Is there a relationship between job satisfaction, as measured by the JSS, and income, measured in dollars? In particular, how does job satisfaction relate to income?
Assumptions
For the Pearson r correlation, both variables should be normally distributed, since normally distributions exhibit a bell-shaped curve. Additionally, other key assumptions include linearity and homoscedasticity. Linearity assumes a straight line relationship between each of the two variables, while homoscedasticity assumes that data is equally distributed about the regression line.
Key Terms
In particular, Cohen’s standard may be used to evaluate the correlation coefficient, which helps determine the strength of the relationship, or the effect size. In particular, correlation coefficients between .10 and .29 represent a small association, whereas coefficients between .30 and .49 represent a medium association, and coefficients of .50 and above represent a large association or relationship.
Continuous data:
Data that is interval or ratio level. Furthermore, this type of data possesses the properties of magnitude and equal intervals between adjacent units. Specifically, an equal intervals between adjacent units means that there are equal amounts of the variable being measured between adjacent units on the scale. For example, consider age: An increase in age from 21 to 22 would be the same as an increase in age from 60 to 61.
Kendall rank correlation:
Similarly, Kendall rank correlation is a non-parametric test that measures the strength of dependence between two variables. If we consider two samples, a and b, where each sample size is n, we know that the total number of pairings with a b is n(n-1)/2. The following formula is used to calculate the value of Kendall rank correlation:
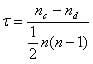
Nc= number of concordant
Nd= Number of discordant
Key Terms
Concordant: Ordered in the same way.
Discordant: Ordered differently.
Spearman rank correlation:
Spearman rank correlation is a non-parametric test that measures the degree of association between two variables. Moreover, the Spearman rank correlation test does not carry any assumptions about the distribution of the data. It is the appropriate correlation analysis when one measure the variables on a scale that is at least ordinal.
The following formula is used to calculate the Spearman rank correlation:
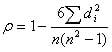
ρ= Spearman rank correlation
di= the difference between the ranks of corresponding variables
n= number of observations
Types of research questions a Spearman Correlation can examine:
Is there a statistically significant relationship between participants’ level of education (high school, bachelor’s, or graduate degree) and in other words, does the level of education impact the starting salary?
Similarly, is there a statistically significant relationship between horse’s finishing position a race and horse’s age?
Assumptions
The assumptions of the Spearman correlation are that data must be at least ordinal and the scores on one variable must be monotonically related to the other variable.
Key Terms
Effect size: In particular, Cohen’s standard may help to evaluate the correlation coefficient to determine the strength of the relationship, or the effect size. Specifically, correlation coefficients between .10 and .29 represent a small association, coefficients between .30 and .49 represent a medium association, and coefficients of .50 and above represent a large association or relationship.
Ordinal data: In an ordinal scale, the levels of a variable are ordered such that one level can be considered higher/lower than another. However, the magnitude of the difference between levels is not necessarily known. For instance, rank ordering levels of education provide a clear example. A graduate degree is higher than a bachelor’s degree, and a bachelor’s degree is higher than a high school diploma. However, we cannot quantify how much higher a graduate degree ranks compared to a bachelor’s degree. We also cannot say that the difference in education between a graduate degree and a bachelor’s degree is the same as the difference between a bachelor’s degree and a high school diploma.
Correlation Resources:
Algina, J., & Keselman, H. J. (1999). Comparing squared multiple correlation coefficients: Examination of a confidence interval and a test significance. Psychological Methods, 4(1), 76-83.
Bobko, P. (2001). Correlation and regression: Applications for industrial organizational psychology and management (2nd ed.). Thousand Oaks, CA: Sage Publications. View
Bonett, D. G. (2008). Meta-analytic interval estimation for bivariate correlations. Psychological Methods, 13(3), 173-181.
Chen, P. Y., & Popovich, P. M. (2002). Correlation: Parametric and nonparametric measures. Thousand Oaks, CA: Sage Publications. View
Cheung, M. W. -L., & Chan, W. (2004). Testing dependent correlation coefficients via structural equation modeling. Organizational Research Methods, 7(2), 206-223.
Coffman, D. L., Maydeu-Olivares, A., Arnau, J. (2008). Asymptotic distribution free interval estimation: For an intraclass correlation coefficient with applications to longitudinal data. Methodology, 4(1), 4-9.
Cohen, J., Cohen, P., West, S. G., & Aiken, L. S. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. (3rd ed.). Mahwah, NJ: Lawrence Erlbaum Associates. View
Hatch, J. P., Hearne, E. M., & Clark, G. M. (1982). A method of testing for serial correlation in univariate repeated-measures analysis of variance. Behavior Research Methods & Instrumentation, 14(5), 497-498.
Kendall, M. G., & Gibbons, J. D. (1990). Rank Correlation Methods (5th ed.). London: Edward Arnold. View
Krijnen, W. P. (2004). Positive loadings and factor correlations from positive covariance matrices. Psychometrika, 69(4), 655-660.
Shieh, G. (2006). Exact interval estimation, power calculation, and sample size determination in normal correlation analysis. Psychometrika, 71(3), 529-540.
Stauffer, J. M., & Mendoza, J. L. (2001). The proper sequence for correcting correlation coefficients for range restriction and unreliability. Psychometrika, 66(1), 63-68.
Related Pages: