What is Hierarchical Linear Modeling?
Hierarchical linear modeling (HLM), also known as multilevel modeling, is a type of statistical analysis that can be applied to data that have a hierarchical or nested structure. In this context, we consider data to have a “hierarchical” structure if individual cases (e.g., participants) come from meaningful groups or clusters. A common example of hierarchical data is in educational research wherein students may be grouped by classroom and/or school.
Example
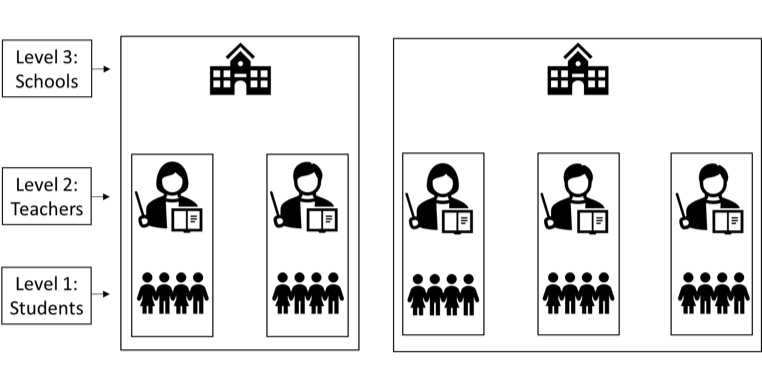
The figure above illustrates this exampIe. In this example we have a three-level data structure: students at Level 1, teachers at Level 2, and schools at Level 3. Data from individual students represent the lowest level of the analysis (Level 1). At Level 1, we might have data such as students’ test scores and demographic characteristics (gender, race, etc.). Students who have the same teacher may be grouped together at Level 2. The figure above depicts five groups of students, each with one teacher. We want to group the students by teacher because students who have the same teacher may be more similar to each other on important variables (such as their test scores) than students with different teachers. We can also include variables that are measured at Level 2, such as the teachers’ years of teaching experience. Finally, students and teachers from the same school may be further grouped together at Level 3.
In the above example, we have two schools: one with two teachers and the other with three teachers. Just as with the student and teacher-level data, we can also include variables measured at the school level, such as school size and the principals’ years of experience.
Students within classrooms and schools is just one example of hierarchical data. Other examples include patients, nurses and doctors grouped by hospital, employees grouped by company, or individuals grouped by family or household. In most research situations, the data will have only two or three levels; however, it is possible to analyze data with more than three levels.
HLM allows us to estimate relationships between variables at multiple levels while accounting for the hierarchical structure of the data. However, it is worth noting that HLM can be used to account for hierarchical data even if all of the variables used in the analysis are measured at Level 1. The reason why we want to account for the data structure is because more basic analyses (e.g., linear regression) assume that all of the observations in the data are independent. If there are groups of observations in the data that are systematically related (e.g., groups of students belonging to the same classroom or school), the assumption of independent observations is violated. Analyses that rely on this assumption may produce biased results when performed on hierarchical data.
Final Remarks
Most major statistical software packages (including SPSS and Intellectus Statistics) are capable of performing HLM. This analysis is a case of mixed-effect modeling, and can be performed in SPSS using the MIXED command. Intellectus Statistics has an analysis option dedicated to HLM and is capable of analyzing two-level data.

We work with graduate students every day and know what it takes to get your research approved.
- Address committee feedback
- Roadmap to completion
- Understand your needs and timeframe