Testing Assumptions of Linear Regression in SPSS
Starting on the journey of regression analysis in SPSS after collecting your data is a pivotal moment in any research project. Having meticulously prepared your dataset, as outlined in our guide on data cleaning and management in SPSS, you’re poised to delve into the regression analysis. However, diving directly into interpreting the regression results without a proper check on the underlying assumptions can lead to misleading conclusions. Let’s demystify the essential assumptions of normality, linearity, homoscedasticity, and the absence of multicollinearity, guiding you through each step with clarity.
Normality of Residuals: The foundation of valid regression analysis lies in the normal distribution of residuals – the differences between the observed and predicted values of the dependent variable. A normal Predicted Probability (P-P) plot serves as a diagnostic tool, where a normal distribution of residuals aligns closely with the plot’s diagonal line. We’ll illustrate how to interpret this plot effectively later on.
Regression help?
Option 1: User-friendly Software
Transform raw data to written interpreted results in seconds.
Option 2: Professional Statistician
Collaborate with a statistician to complete and understand your results.
Homoscedasticity: This assumption concerns the distribution of residuals. For your data to be homoscedastic, the residuals should be evenly spread across the range of predicted values, resembling a “shotgun blast” of points. This uniform distribution ensures that the variance of errors is constant. Heteroscedasticity, the opposite condition, manifests as a patterned spread of residuals (e.g., cone or fan-shaped), indicating variance inconsistency. We will guide you on how to visually assess homoscedasticity through a scatterplot of predicted values against residuals.
Linearity: The assumption of linearity posits a direct, straight-line relationship between predictor and outcome variables. If the residuals are normally distributed and exhibit homoscedasticity, linearity typically holds, simplifying the analysis process.Multicollinearity refers to when your predictor variables are highly correlated with each other. This is an issue, as your regression model will not be able to accurately associate variance in your outcome variable with the correct predictor variable, leading to muddled results and incorrect inferences. Keep in mind that this assumption is only relevant for a multiple linear regression, which has multiple predictor variables. If you are performing a simple linear regression (one predictor), you can skip this assumption.
Absence of Multicollinearity: In multiple linear regression, where several predictor variables are involved, multicollinearity can obscure the distinct impact of each predictor. This phenomenon occurs when predictors are highly correlated with one another, complicating the attribution of variance in the outcome variable. Multicollinearity assessment can be approached through two methods:
- Correlation Coefficients: By constructing a correlation matrix among predictors, coefficients nearing or exceeding .80 indicate strong correlations, suggesting multicollinearity.
- Variance Inflation Factor (VIF): VIF values offer a quantitative measure of multicollinearity, with values below 5.00 indicating minimal concern, and those exceeding 10.00 signaling significant multicollinearity.
To fully check the assumptions of the regression using a normal P-P plot, a scatterplot of the residuals, and VIF values, bring up your data in SPSS and select Analyze –> Regression –> Linear. Set up your regression as if you were going to run it by putting your outcome (dependent) variable and predictor (independent) variables in the appropriate boxes.
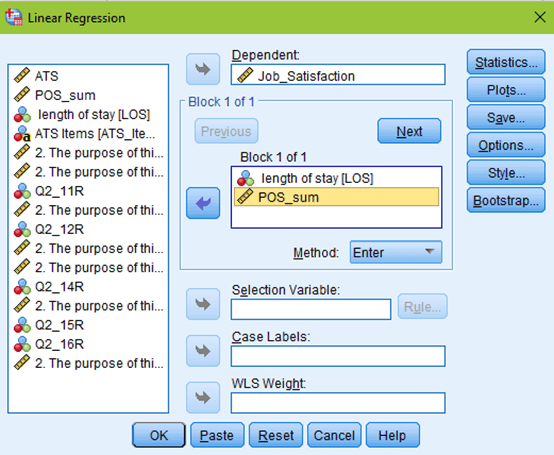
But don’t click OK yet! Click the Statistics button at the top right of your linear regression window. Estimates and model fit should automatically be checked. Now, click on collinearity diagnostics and hit continue.
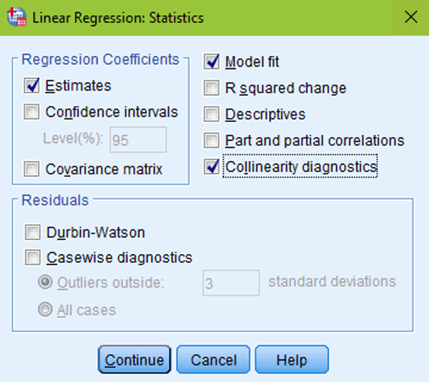
The next box to click on would be Plots. You want to put your predicted values (*ZPRED) in the X box, and your residual values (*ZRESID) in the Y box. Also make sure that normal probability plot is checked, and then hit continue.
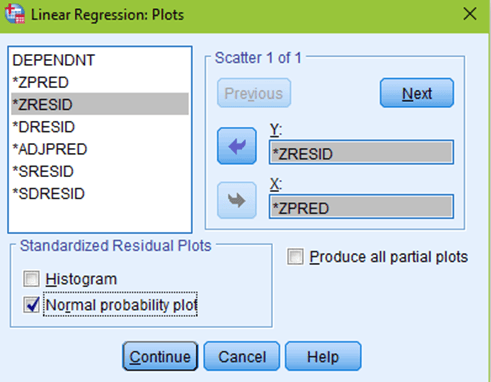
Now you are ready to hit OK! You will get your normal regression output, but you will see a few new tables and columns, as well as two new figures. First, you will want to scroll all the way down to the normal P-P plot. You will see a diagonal line and a bunch of little circles. Ideally, your plot will look like the two leftmost figures below. If your data is not normal, the little circles will not follow the normality line, such as in the figure to the right. Sometimes, there is a little bit of deviation, such as the figure all the way to the left. That is still ok; you can assume normality as long as there are no drastic deviations.
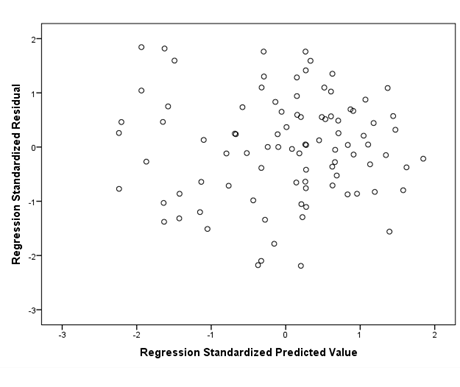
The next assumption to check is homoscedasticity. The scatterplot of the residuals will appear right below the normal P-P plot in your output. Ideally, you will get a plot that looks something like the plot below. The data looks like you shot it out of a shotgun—it does not have an obvious pattern, there are points equally distributed above and below zero on the X axis, and to the left and right of zero on the Y axis.
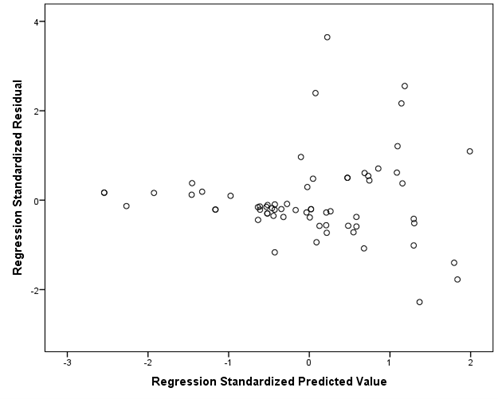
If your data is not homoscedastic, it might look something like the plot below. You have a very tight distribution to the left of the plot, and a very wide distribution to the right of the plot. If you were to draw a line around your data, it would look like a cone.
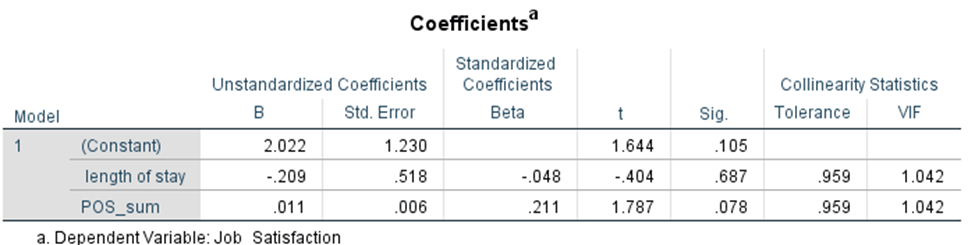
Finally, you want to check absence of multicollinearity using VIF values. Scroll up to your Coefficients table. All the way at the right end of the table, you will find your VIF values. Each value is below 10, indicating that the assumption is met.
You will want to report the results of your assumption checking in your results chapter, although school guidelines and committee preferences will ultimately determine how much detail you share. It is always best to err on the side of caution, and include the APA-formatted figures as well as your VIF values in your results chapter. After testing these assumptions, you will be ready to interpret your regression!
Intellectus allows you to conduct and interpret your analysis in minutes. Assumptions are pre-loaded, and output is provided in APA style complete with tables and figures. Click ‘Try Now’ below to create a free account, and get started analyzing your data now!