Effect Size
Effect size is a statistical concept that measures the strength of the relationship between two variables on a numeric scale. For instance, if we have data on the height of men and women and we notice that, on average, men are taller than women, the difference between the height of men and the height of women is known as the effect size. The greater the effect size, the greater the height difference between men and women will be. Statistic effect size helps us in determining if the difference is real or if it is due to a change of factors. In hypothesis testing, effect size, power, sample size, and critical significance level are related to each other. In Meta-analysis, effect size is concerned with different studies and then combines all the studies into single analysis. In statistics analysis, the effect size is usually measured in three ways: (1) standardized mean difference, (2) odd ratio, (3) correlation coefficient.
Types of effect size
Pearson r correlation: Pearson r correlation was developed by Karl Pearson, and it is most widely used in statistics. This parameter of effect size is denoted by r. The value of the effect size of Pearson r correlation varies between -1 to +1. According to Cohen (1988, 1992), the effect size is low if the value of r varies around 0.1, medium if r varies around 0.3, and large if r varies more than 0.5. The Pearson correlation is computed using the following formula:
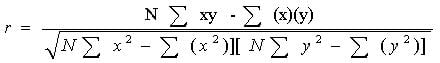
Where
r = correlation coefficient
N = number of pairs of scores
∑xy = sum of the products of paired scores
∑x = sum of x scores
∑y = sum of y scores
∑x2= sum of squared x scores
∑y2= sum of squared y scores
Need help with your research?
Schedule a time to speak with an expert using the calendar below.
Standardized means difference: When a research study is based on the population mean and standard deviation, then the following method is used to know the effect size:
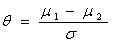
The effect size of the population can be known by dividing the two population mean differences by their standard deviation.
Cohen’s d Cohen’s d is known as the difference of two population means and it is divided by the standard deviation from the data. Mathematically Cohen’s effect size is denoted by:
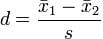
Where s can be calculated using this formula:
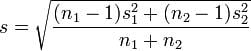
Glass’s Δ method: This method is similar to the Cohen’s method, but in this method standard deviation is used for the second group. Mathematically this formula can be written as:
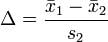
Hedges’ g method: This method is the modified method of Cohen’s d method. Hedges’ g method of effect size can be written mathematically as follows:
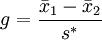
Where standard deviation can be calculated using this formula:
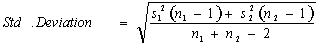
Cohen’s f2 method: Cohen’s f2 method measures the effect size when we use methods like ANOVA, multiple regression, etc. The Cohen’s f2 measure effect size for multiple regressions is defined as the following:
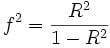
Where R2 is the squared multiple correlation.
Cramer’s φ or Cramer’s V method: Chi-square is the best statistic to measure the effect size for nominal data. In nominal data, when a variable has two categories, then Cramer’s phi is the best statistic use. When these categories are more than two, then Cramer’s V statistics will give the best result for nominal data.
Odd ratio: The odds ratio is the odds of success in the treatment group relative to the odds of success in the control group. This method is used in cases when data is binary. For example, it is used if we have the following table:
| Frequency | ||
| Success | Failure | |
| Treatment group | a | b |
| Control group | c | d |
To measure the effect size of the table, we can use the following odd ratio formula:
Related Pages:
To reference this page: Statistics Solutions. (2013). Effect Size . Retrieved from https://www.statisticssolutions.com/academic-solutions/resources/directory-of-statistical-analyses/effect-size/
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
- Edit your research questions and null/alternative hypotheses
- Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
- Justify your sample size/power analysis, provide references
- Explain your data analysis plan to you so you are comfortable and confident
- Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
- Clean and code dataset
- Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
- Conduct analyses to examine each of your research questions
- Write-up results
- Provide APA 6th edition tables and figures
- Explain chapter 4 findings
- Ongoing support for entire results chapter statistics