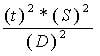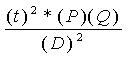Sample Size Calculation
Sample size calculation plays a very important role in statistical analysis. Sample size calculation refers to how much data we need for particular research to make a correct decision. If we have more data, then our decision will be more accurate, and there will be less error of the parameter estimate. Some of the factors that affect the sample size calculation are the type of data, including the power of the sample size, the Technique used for analysis, the marginal error, the level of significance, the standard deviation, the missing value, etc. First of all, we should consider the type of data level and the measurement of a specific sample size.There are four types of data levels:

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
- nominal data;
- ordinal data;
- interval data; and
- ratio data.
Nominal data is simply categorical data. Ordinal data is the data in which ranks are assigned to the data. Interval data is when an interval is given between the cases. Ratio data is metric or continuous data, on which we can perform all analysis which cannot be performed on nominal, ordinal, or interval data. In determining the sample size calculation, we should consider the level of significance or the level of alpha. For instance, two tailed test alpha level is 5%, which is equal to 1.96. When the sample size calculation is done, we should consider the marginal error as well. Marginal error is simply the error that a researcher is willing to accept for a particular sample size. For example, in continuous data t value of alpha for 5% is 1.96 and SD in population is 1.167, and marginal error is .21. Then we can calculate the sample size by using the following formula:
N=
N= sample size
t= level of alpha
S= standard deviation
D= marginal error
When the data is categorical, then we can use the probability of method instead of the standard deviation. For example, when we have two categories for samples, then we can use .5 probability of the first category and .5 probability for the second category. We can use the following formula in the case of categorical data:
t= level of alpha
P= probability of event happening
Q= probability of second event happening
D= marginal error
These are some basic formulas for sample size calculation. But sample size calculation differs from technique to technique. For example, when we are comparing the means of two populations, if the sample size is less than 30, then we will use the t-test. If the sample size is greater than 30, then we will use the Z-test for comparing the two populations’ sample means. As a rule of thumb, in regression analysis, there should be 10 cases for each independent variable. For example, if we have two independent variables, then the minimum sample size should be 20 in order to reach a correct decision about the regression parameter. If the sample size is less than the given criteria, then the decision will not be correct. When data are categorical and the level of alpha decreases, then the sample size should be bigger for the same technique. If the population size is smaller, then we need a bigger sample size, and if the population is large, then we need a smaller sample size as compared to the small population. Sample size will differ with different margin error. Missing value also affects the sample size. When data has missing value, we need bigger sample sizes as compared to the non-missing value sample. In an analysis of variance test, we need to determine how many covariates we can use for a particular treatment variable. We can use sample size to determine the covariate. For example, with a sample size of 50, and a number of groups in 3 treatment factor, we can use only 3 covariates in an analysis of variance study. Variance also affects the sample size. When variance is more for the variable taken into study, then the sample size needs to be bigger to reach a correct decision about the parameter estimate. When we do not know the population standard deviation, then we can use the range to know the standard deviation. Sample size also depends on the power. With more power, we need a bigger sample size.
For information on statistical consulting services, click here.
Intellectus allows you to generate your sample size write up in seconds. Click the link below to create a free account, and get started now!