Conduct and Interpret a Repeated Measures ANCOVA
What is the Repeated Measures ANCOVA?
The repeated measures ANCOVA, part of the General Linear Model (GLM) family, is a sophisticated statistical analysis designed for a specific purpose: comparing average scores across different conditions or times. At its core, ANCOVA stands for Analysis of Covariance, which blends the comparison of means (like in ANOVA) with the adjustment for other variables, known as covariates, that might influence the outcome.
This method is important when you need to understand changes or differences in mean scores from the same subjects over multiple observations or time points, all while accounting for potential confounding variables that could skew the results. Essentially, it allows for a cleaner, more accurate comparison by adjusting for these covariates.
In practice, a repeated measures ANCOVA model can handle not just one, but potentially several independent variables, and it can adjust for up to ten covariate factors. This flexibility makes it a powerful tool for researchers. At its most basic, the model requires at least one dependent variable (what you’re measuring) that has been observed more than once, and one covariate (a variable that could influence the outcome you’re trying to measure).
By using repeated measures ANCOVA, researchers can gain insights into how and why scores change over time or across conditions, providing a deeper understanding of the dynamics at play, all while controlling for variables that could introduce bias into the analysis.
Example:
A research team wants to test the user acceptance of a new online travel booking tool. The team conducts a study where they assign 30 randomly chosen people into two groups. One group that uses the new system and another group acts as a control group and books its travel via phone. The team also records self-reported computer literacy of each user.
The team measures the user acceptance of the system as the behavioral intention to use the system in the first four weeks after it went live. Since user acceptance is a latent behavioral construct the researchers measure it with three items – ease of use, perceived usefulness, and effort to use. They now use the repeated measures ANCOVA to find out if the weekly measurements differ significantly from each other, if the treatment and control group differ significantly from each other all the time controlling for the influence of computer literacy.
When faced with a question similar to the one in our example, try to run 4 MANCOVAs to test the influence of the independent variables on each of the observations of the four weeks while controlling for the covariate. Keep in mind, running multiple ANOVAs does not account for individual differences in baselines of the participants of the study. Technically, the assumption of independence is violated because the numbers of week two are not completely independent from the numbers from week one.
Need help with your analysis?
Schedule a time to speak with an expert using the calendar below.
User-friendly Software
Transform raw data to written, interpreted, APA formatted results in seconds.
The repeated measures ANCOVA is similar to the dependent sample t-Test, and the repeated measures ANOVA because it also compares the mean scores of one group to another group on different observations. It is necessary for the repeated measures ANCOVA that the cases in one observation are directly linked with the cases in all other observations. This automatically happens when repeated measures are taken, or when analyzing similar units or comparable specimen.
Both strategies (pairing of observations or making repeated measurements) are very common when conducting experiments or making observations with time lags. Pairing the observed data points is typically done to exclude any cofounding or hidden factors (cf. partial correlation). It is also used to account for individual differences in the baselines, for example pre-existing conditions in clinical research. Consider the example of a drug trial where the participants have individual differences that might have an impact on the outcome of the trial. The typical drug trial splits all participants into a control and the treatment group and measures the effect of the drug in months 1 – 18. The repeated measures ANCOVA can correct for the individual differences or baselines. The baseline differences that might have an effect on the outcome could be a typical parameter like blood pressure, age, or gender. Not only does the repeated measures ANCOVA account for difference in baselines, but also for effects of confounding factors. This allows the analysis of interaction effects between the covariate, the time and the independent variables’ factor levels.
Since the pairing is explicitly defined and thus new information added to the data, paired data can always be analyzed with a regular ANCOVA, but not vice versa. The baseline differences, however, will not be accounted for.
The Repeated Measures ANCOVA in SPSS
Consider the following research question:
Are there individual differences in the longitudinal measures of aptitude between students who passed the final exam and the students who failed the final exam; when we control for the mathematical abilities as measured by the standardized test score of the math test?
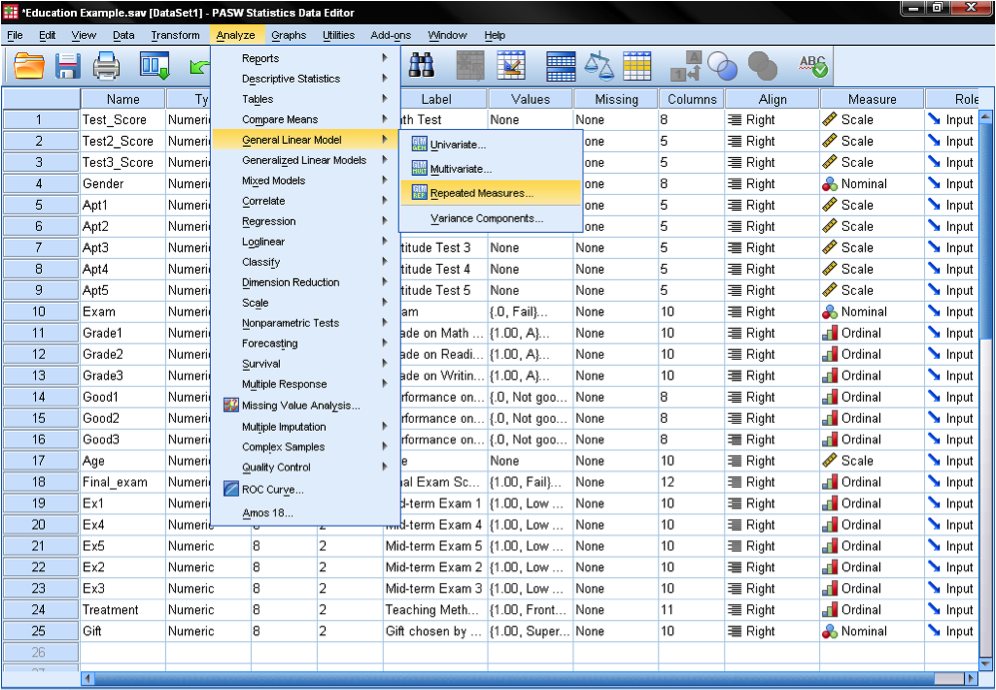
The repeated measures ANCOVA uses the GLM module of SPSS, like the factorial ANOVAs, MANOVAs, and MANCOVAS. The repeated measures ANCOVA can be found in SPSS in the menu Analyze/General Linear Model/Repeated Measures…
The dialog box that opens is different than the GLM module you might know from the MANCOVA. Before specifying the model we need to group the repeated measures.
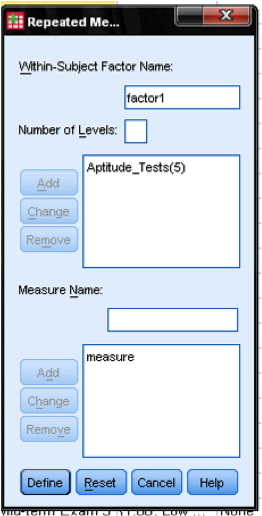
This is done by creating a within-subject factor. It is called a within subject factor of our repeated measures ANCOVA because it represents the different observations of one subject. We measured the aptitude on five different data points, which creates five factor levels. We specify a factor called Aptitude_Tests with five factor levels (that is the number of our repeated observations).
Since our research question also requires investigation as to the difference between the students who failed the final exam and the students who passed the final exam, we will include a measurement in the model.
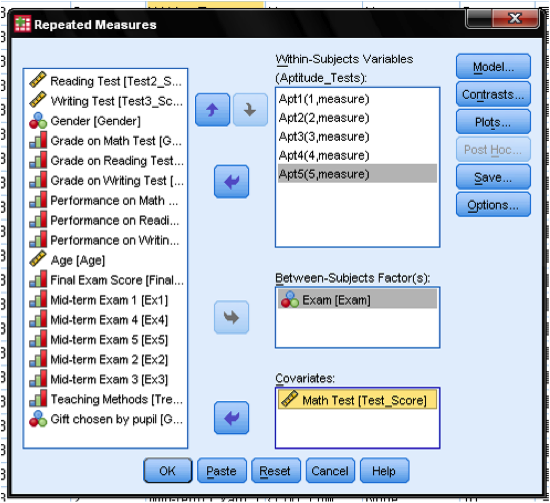
The next dialog box allows us to specify the repeated measures ANCOVA. First we need to add the five observation points to the within-subject variables. Then, we need to add Exam (fail versus pass group of students) to the list of between-subject factors. Lastly, we add the results of the math test to the list of covariates.
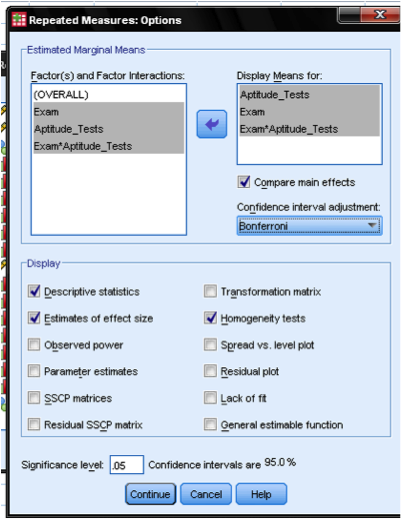
As usual we go with the standard settings for the model, contrast, plots, and save the results. Also note that Post Hoc tests are disabled because of the inclusion of a covariate in the model.
We simply add some useful statistics to the repeated measures ANOVA output in the Options… dialog. These include the comparison of main effects with adjusted degrees of freedom, some descriptive statistics, the practical significance eta, and the Levene test for homoscedasticity since we included Exam as an independent variable in the analysis.
Need More Help?
Check out our online course for conducting a repeated measures ANCOVA here.