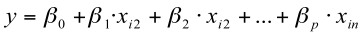Conduct and Interpret an Ordinal Regression
What is Ordinal Regression?
Ordinal regression is a member of the family of regression analyses. As a predictive analysis, ordinal regression describes data and explains the relationship between one dependent variable and two or more independent variables. In ordinal regression analysis, the dependent variable is ordinal (statistically it is polytomous ordinal) and the independent variables are ordinal or continuous-level (ratio or interval).
Sometimes the dependent variable is also called response, endogenous variable, prognostic variable or regressand. The independent variables are also called exogenous variables, predictor variables or regressors.
Linear regression estimates a line to express how a change in the independent variables affects the dependent variables. The independent variables are added linearly as a weighted sum of the form.
Linear regression estimates the regression coefficients by minimizing the sum of squares between the left and the right side of the regression equation. Ordinal regression however is a bit trickier. Let us consider a linear regression of income = 15,000 + .980 * age. We know that for a 30 year old person the expected income is 44,400 and for a 35 year old the income is 49,300. That is a difference of 4,900. We also know that if we compare a 55 year old with a 60 year old the difference of 68,900-73,800 = 4,900 is exactly the same difference as the 30 vs. 35 year old. This however is not always true for measures that have ordinal scale. For instance if we classify the income to be low, medium, high, it is impossible to say if the difference between low and medium is the same as between medium and high, or if 3*low = high.
There are three major uses for Ordinal Regression Analysis: 1) causal analysis, 2) forecasting an effect, and 3) trend forecasting. Other than correlation analysis for ordinal variables (e.g., Spearman), which focuses on the strength of the relationship between two or more variables, ordinal regression analysis assumes a dependence or causal relationship between one or more independent and one dependent variable. Moreover the effect of one or more covariates can be accounted for.
Firstly, ordinal regression might be used to identify the strength of the effect that the independent variables have on a dependent variable. A typical question is, “What is the strength of relationship between dose (low, medium, high) and effect (mild, moderate, severe)?”
Secondly, ordinal regression can be used to forecast effects or impacts of changes. That is, ordinal regression analysis helps us to understand how much will the dependent variable change, when we change the independent variables. A typical question is, “When is the response most likely to jump into the next category?”
Finally, ordinal regression analysis predicts trends and future values. The ordinal regression analysis can be used to get point estimates. A typical question is, “If I invest a medium study effort what grade (A-F) can I expect?”
The Ordinal Regression in SPSS
For ordinal regression, let us consider the research question:
In our study the 107 students have been given six different tests. The pupils either failed or passed the first five tests. For the final exam, the students got graded either as fail, pass, good or distinction. We now want to analyze how the first five tests predict the outcome of the final exam.
To answer this we need to use ordinal regression to analyze the question above. Although technically this method is not ideal because the observations are not completely independent, it best suits the purpose of the research team.
The ordinal regression analysis can be found in Analyze/Regression/Ordinal…
The next dialog box allows us to specify the ordinal regression model. For our example the final exam (four levels – fail, pass, good, distinction) is the dependent variable, the five factors are Ex1 … Ex5 for the five exams taken during the term. Please note that this works correctly only if the right measurement scales have been defined within SPSS.
Furthermore, SPSS offers the option to include one or more covariates of continuous-level scale (interval or ratio). However, adding more than one covariate typically results in a large cell probability matrix with a large number of empty cells.
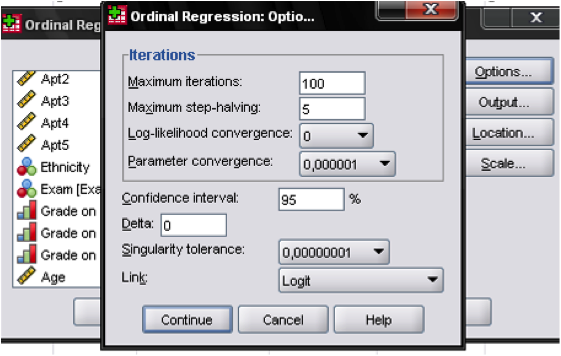
The options dialog allows us to manage various settings for the iteration solution, more interestingly here we can also change the link setting for the ordinal regression. In ordinal regression the link function is a transformation of the cumulative probabilities of the ordered dependent variable that allows for estimation of the model. There are five different link functions.
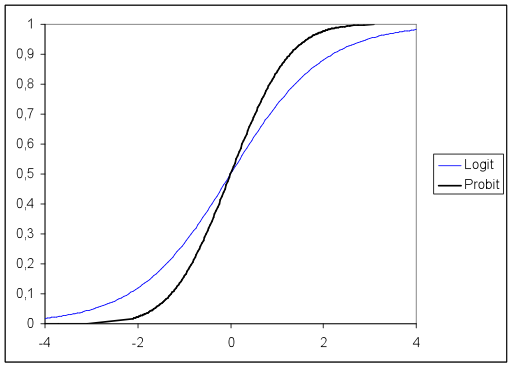
Both models (logit and probit) are most commonly used in ordinal regression, in most cases a model is fitted with both functions and the function with the better fit is chosen. However, probit assumes normal distribution of the probability of the categories of the dependent variable, when logit assumes the log distribution. Thus the difference between logit and probit is typically seen in small samples.
3. Negative log-log: This link function is recommended when the probability of the lower category is high. Mathematically the negative log-log is p(z) = –log (– log(z)).
4. Complementary log-log: This function is the inverse of the negative log-log function. This function is recommended when the probability of higher category is high. Mathematically complementary log-log is p(z) = log (– log (1 – z)).
5. Cauchit: This link function is used when the extreme values are present in the data. Mathematically Cauchit is p(z) = tan (p(z – 0.5)).
We leave the ordinal regression’s other dialog boxes at their default settings; we just add the test of parallel lines in the Output menu.