Conduct and Interpret a Factorial ANCOVA

Adding covariates to a factorial ANCOVA can increase its power by explaining more variability. However, overfitting can occur—more covariates reduce degrees of freedom and may decrease statistical power, especially if the covariate is weak.

The factorial ANCOVA removes the covariate’s effect and tests the relationship, similar to partial correlation.

The factorial ANCOVA needs at least four variables (the simplest case with two factors is called two-way ANCOVA):

• Two or more independent variables group cases into four or more groups, with the independent variable being at least nominal.
• The independent variable influences the dependent variable. It has to be of continuous-level scale (interval or ratio data).  Also, it needs to be homoscedastic and multivariate normal
• The covariate, or confounding factor, moderates the effect of the independent variable on the dependent variable. It must be continuous (interval or ratio data) and is often a pre-test or baseline value in ANCOVA.

Typical questions the factorial ANCOVA answers are as follows:

• Medicine – Does a drug work? A factorial ANCOVA can test life expectancy differences between the groups, accounting for dose and covariates like lifestyle and age.
• Sociology – Are rich people living in the countryside happier? Do different income classes report a significantly different satisfaction with life when looking where they live (urban, suburban, rural)? This can be answered with a factorial ANOVA or ANCOVA, which controls for factors like marital status and job satisfaction.
• Management Studies – Which brands from the BCG matrix have a higher customer loyalty? The BCG matrix measures brands in a brand portfolio with their business growth rate (high/low) and their market share (high/ low).  A factorial ANOVA answers the question to which brand are customers more loyal – stars, cash cows, dogs, or question marks? And a factorial ANCOVA can control for confounding factors, like satisfaction with the brand or appeal to the customer.

The Factorial ANCOVA in SPSS

The Factorial ANCOVA in SPSS’s GLM allows up to 10 covariates. Without covariates, it works like a Factorial ANOVA. Correctly defining measurement levels is essential for accurate results.

We want to see if gender and exam outcome affect math scores, controlling for reading ability. Outcome affect math scores, controlling for reading ability from a standardized test.

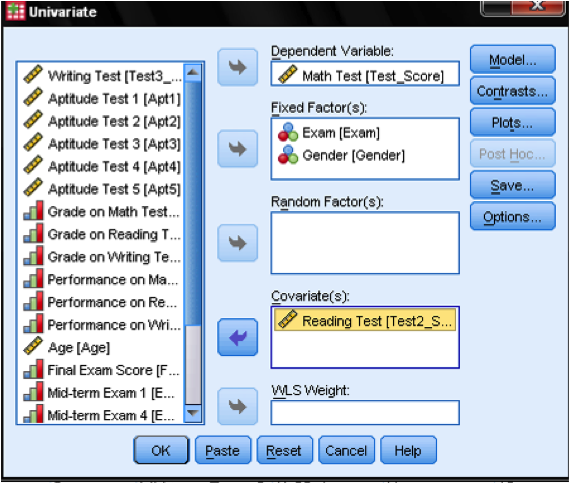
The Factorial ANCOVA can be found in Analyze/General Linear Model/Univariate…

This opens the GLM dialog, which allows us to specify any linear model.  To answer our research question we need to add the independent variables (Exam and Gender) to the list of fixed factors.

[Remember that the factor is fixed if it is deliberately manipulated and not just randomly drawn from a population.  In our ANCOVA example this is the case.  This also makes the ANCOVA the model of choice when analyzing semi-partial correlations in an experiment, instead of the partial correlation analysis with requires random data.]

The Dependent Variable is the Math Test, and the Covariate is the Reading Test.

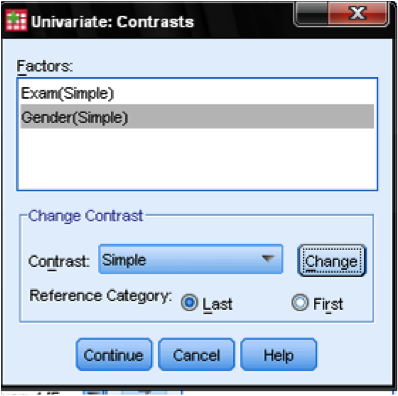
In the dialog box Model… we leave all settings on the default.  The default for all GLM (including the Factorial ANCOVA) is the full factorial model.  The field post hocs is disabled when one or more covariates are entered into the analysis.  If we want to include a group comparison into our factorial ANCOVA we can add contrast to the analysis.

If we want to compare all groups against a specific group we need to select Simple as the Contrast Method, and we also need to specify which group (either the first or the last) should be compared against all other groups.  However, since in this example both of our fixed factors only have two factor levels (male/female and pass/fail) we do not really need contrasts to answer the research question.