Conduct and Interpret a (Pearson) Bivariate Correlation
What is a Bivariate (Pearson) Correlation?
Bivariate Correlation is a widely used term in statistics. In fact, it entered the English language in 1561, 200 years before most of the modern statistic tests were discovered. It is derived from the Latin word correlation, which means relation. Correlation generally describes the effect that two or more phenomena occur together and therefore they are linked. Many academic questions and theories investigate these relationships. Is the time and intensity of exposure to sunlight related the likelihood of getting skin cancer? Are people more likely to repeat a visit to a museum the more satisfied they are? Do older people earn more money? Are wages linked to inflation? Do higher oil prices increase the cost of shipping? It is very important, however, to stress that correlation does not imply causation.

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
A correlation expresses the strength of linkage or co-occurrence between two variables in a single value between -1 and +1. This value that measures the strength of linkage is called correlation coefficient, which is represented typically as the letter r.
The correlation coefficient between two continuous-level variables is also called Pearson’s r or Pearson product-moment correlation coefficient. A positive r value expresses a positive relationship between the two variables (the larger A, the larger B) while a negative r value indicates a negative relationship (the larger A, the smaller B). A correlation coefficient of zero indicates no relationship between the variables at all. However correlations are limited to linear relationships between variables. Even if the correlation coefficient is zero, a non-linear relationship might exist.
Bivariate (Pearson) Correlation in SPSS
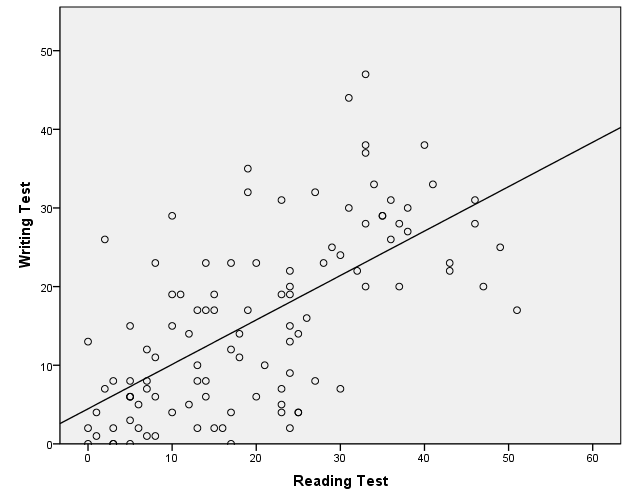
At this point it would be beneficial to create a scatter plot to visualize the relationship between our two test scores in reading and writing. The purpose of the scatter plot is to verify that the variables have a linear relationship. Other forms of relationship (circle, square) will not be detected when running Pearson’s Correlation Analysis. This would create a type II error because it would not reject the null hypothesis of the test of independence (‘the two variables are independent and not correlated in the universe’) although the variables are in reality dependent, just not linearly.
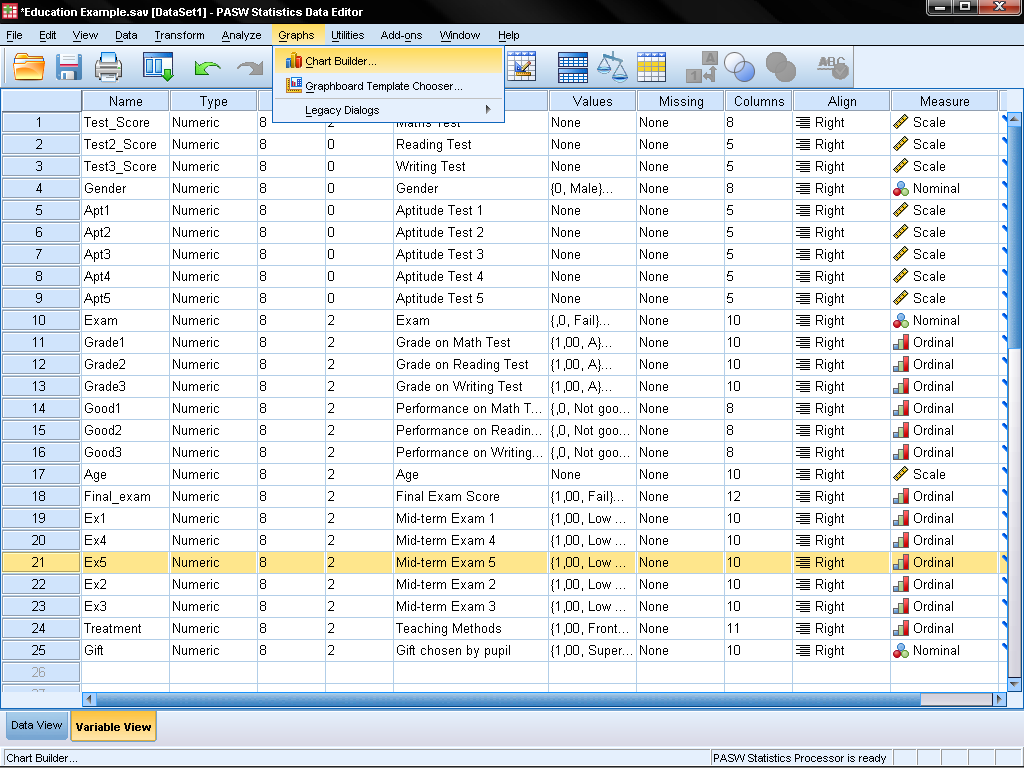
The scatter plot can either be found in Graphs/Chart Builder… or in Graphs/Legacy Dialog/Scatter Dot…
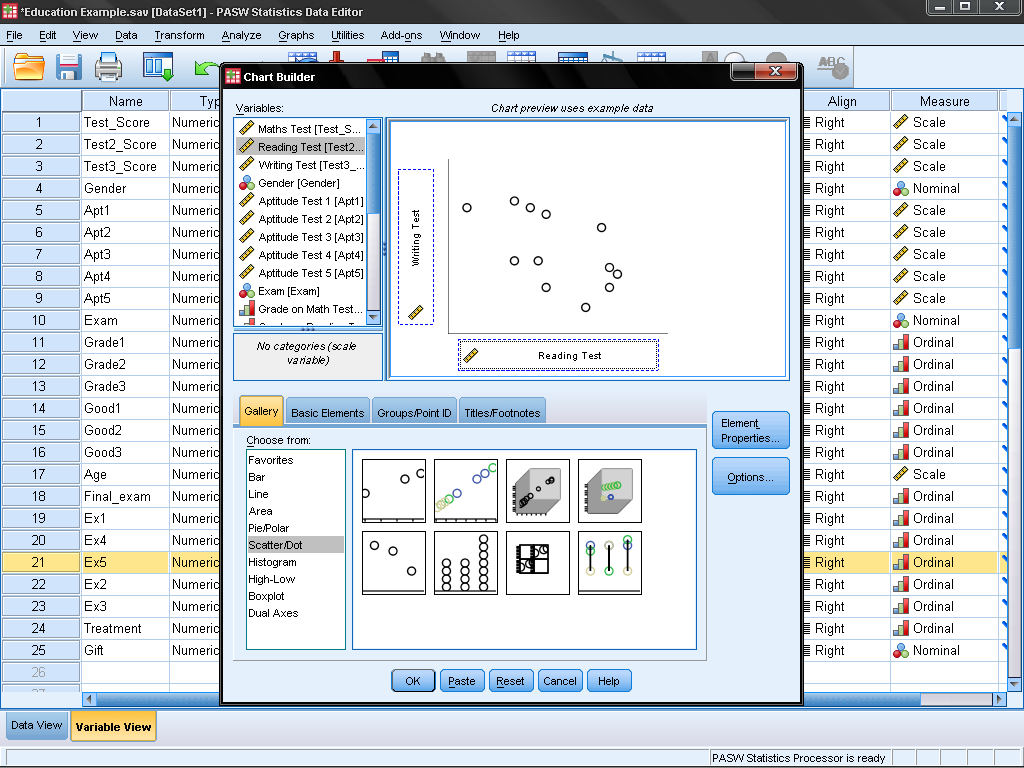
In the Chart Builder we simply choose in the Gallery tab the Scatter/Dotgroup of charts and drag the ‘Simple Scatter’ diagram (the first one) on the chart canvas. Next we drag variable Test_Score on the y-axis and variable Test2_Score on the x-Axis.
SPSS generates the scatter plot for the two variables. A double click on the output diagram opens the chart editor and a click on ‘Add Fit Line’ adds a linearly fitted line that represents the linear association that is represented by Pearson’s bivariate correlation.
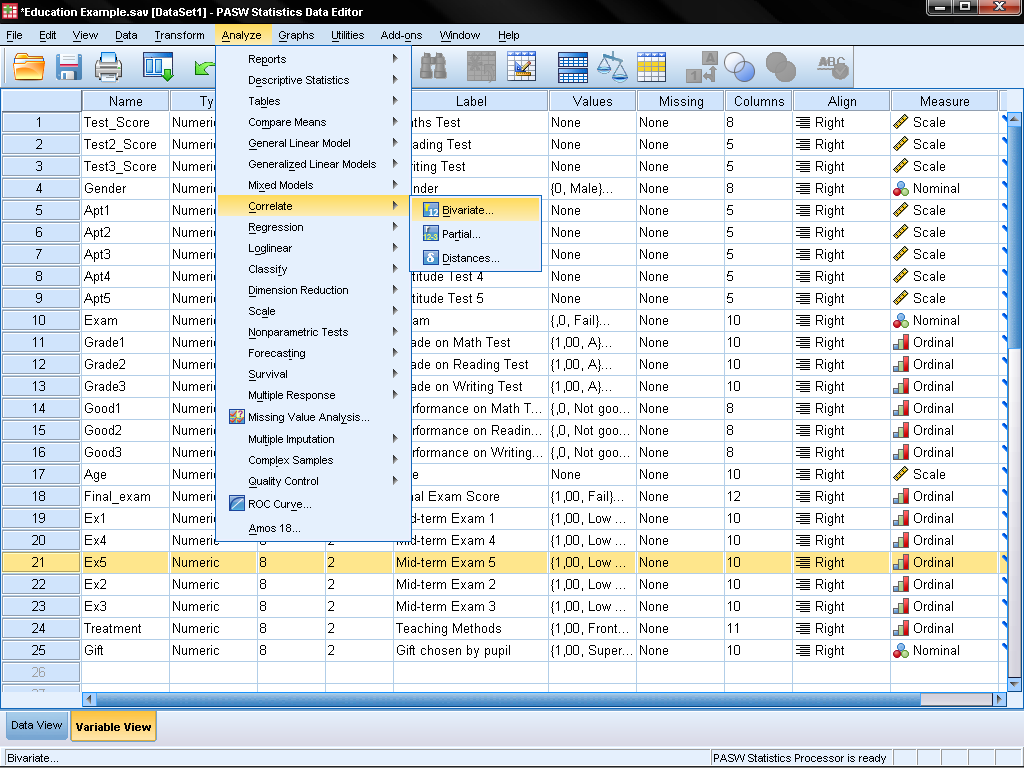
To calculate Pearson’s bivariate correlation coefficient in SPSS we have to open the dialog in Analyze/Correlation/Bivariate…
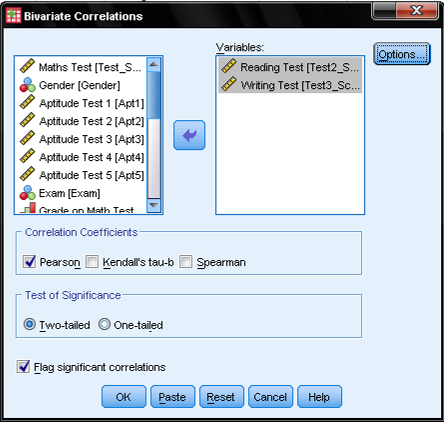
This opens the dialog box for all bivariate correlations (Pearson’s, Kendall’s, Spearman). Simply select the variables you want to calculate the bivariate correlation for and add them with the arrow.
Select the bivariate correlation coefficient you need, in this case Pearson’s. For the Test of Significance we select the two-tailed test of significance, because we do not have an assumption whether it is a positive or negative correlation between the two variables Reading and Writing. We also leave the default tick mark at flag significant correlations which will add a little asterisk to all correlation coefficients with p<0.05 in the SPSS output.
Output, syntax, and interpretation can be found in our downloadable manual: Statistical Analysis: A Manual on Dissertation Statistics in SPSS (included in our member resources). Click here to download.
A correlation expresses the strength of linkage or co-occurrence between to variables in a single value between -1 and +1. This value that measures the strength of linkage is called correlation coefficient, which is represented typically as the letter r.
The correlation coefficient between two continuous-level variables is also called Pearson’s r or Pearson product-moment correlation coefficient. A positive r value expresses a positive relationship between the two variables (the larger A, the larger B) while a negative r value indicates a negative relationship (the larger A, the smaller B). A correlation coefficient of zero indicates no relationship between the variables at all. However correlations are limited to linear relationships between variables. Even if the correlation coefficient is zero, a non-linear relationship might exist.