Understanding the Wilcoxon Sign Test
The Wilcoxon Signed Rank Test offers a non-parametric alternative to the paired sample t-test, specifically designed for comparing the means of two related samples or paired observations. It is particularly useful when the assumptions required for parametric tests, such as the normal distribution of differences between pairs, are not met. Unlike its parametric counterpart, the Wilcoxon Signed Rank Test does not rely on the normal distribution of data, making it suitable for a wider range of data types, including ordinal data.
Key Differences Between Similar Tests
- Mann-Whitney U-test vs. Wilcoxon Signed Rank Test: While both are non-parametric and assess median differences, the Mann-Whitney U-test is used for two independent samples, and the Wilcoxon Signed Rank Test is for two dependent samples.
- Dependent vs. Independent Samples: The Wilcoxon test underscores the dependency aspect by comparing changes within paired or matched samples, assuming that any difference observed is attributable to the manipulation or intervention between the two measurements.
The Role of Dependence in Testing
The Wilcoxon Signed Rank Test, like other dependence tests, operates under the premise that variables can be categorized as independent (predictor) or dependent (outcome). The test evaluates how changes in the independent variable influence the dependent variable, with the independent variable often being a specific intervention or condition that categorizes the sample into different groups or levels.
Mechanism of the Wilcoxon Signed Rank Test
- Comparison Metric: Unlike the t-test, which compares mean scores, the Wilcoxon test uses signed ranks to evaluate differences. This involves ranking the absolute differences between pairs, then assigning signs (+ or -) based on the direction of the difference, and finally analyzing these signed ranks to determine statistical significance.
- Statistical Significance: The test assesses whether the observed pattern of ranks (taking into account their signs) could be due to random chance, with the null hypothesis typically stating that the median difference between pairs is zero.
Conducting and Interpreting the Wilcoxon Signed Rank Test
- Prepare the Data: Pair the observations and calculate the differences between each pair.
- Rank the Differences: Rank the absolute values of these differences, ignoring signs initially.
- Assign Signs to Ranks: Reintroduce the signs to the ranks based on whether the difference was positive or negative.
- Calculate the Test Statistic: Sum the ranks for positive differences and for negative differences, using these sums to calculate the test statistic.
- Interpret the Results: Determine whether the test statistic exceeds the critical value (from Wilcoxon distribution tables) to reject or fail to reject the null hypothesis.
Conclusion
The Wilcoxon Signed Rank Test is an invaluable tool for researchers dealing with non-normally distributed data or ordinal data, providing a robust method for assessing changes or effects within paired samples. Its reliance on signed ranks rather than raw differences offers a unique approach to understanding the impact of interventions or conditions on a dependent variable, making it a critical technique in the arsenal of non-parametric statistical methods.
Wilcoxon Sign Test help?
Option 1: User-friendly Software
Transform raw data to written interpreted results in seconds.
Option 2: Professional Statistician
Collaborate with a statistician to complete and understand your results.
Flexibility of the Wilcoxon Signed Rank Test
The Wilcoxon Signed Rank Test stands out for its flexibility and applicability to a wide array of data types, particularly because it does not presuppose any specific distribution characteristics of the underlying variables. This non-parametric nature renders it especially suitable for analyzing ordinal data or data that do not adhere to the assumptions of multivariate normality, often required by parametric tests like the t-test and F-test.
Mathematical Comparisons and Distinctions
Mathematically, the Wilcoxon Signed Rank Test bears similarities to both the Mann-Whitney U-test (also known as the Wilcoxon 2-sample t-test) and the dependent samples t-test. However, while the dependent samples t-test assesses the average difference between two observations, aiming to determine if this average difference is zero, the Wilcoxon test delves into the distribution of differences, specifically testing whether the median of these differences (reflected through mean signed ranks) is zero. This subtle shift from testing averages to medians enhances the test’s robustness, particularly in the presence of outliers or heavily skewed distributions.
Signed Ranks and Their Implications
The process involves pooling all differences between paired observations, ranking these differences based on their absolute values, and then assigning a sign to each rank corresponding to the direction of the difference (positive or negative). This approach to dealing with differences – termed as “signed ranks” – underpins the methodology of the Wilcoxon Signed Rank Test, distinguishing it from parametric alternatives by focusing on median differences rather than mean differences.
Significance Testing in the Wilcoxon Signed Rank Test
A key assumption for the significance testing of the Wilcoxon Signed Rank Test is that with a sample size of at least ten paired observations, the distribution of the test statistic (the W-value) approximates a normal distribution. This approximation allows researchers to normalize the empirical W-statistics, facilitating a comparison against the z-ratio of the normal distribution to ascertain confidence levels. Such normalization is crucial for interpreting the test outcomes and determining the statistical significance of the observed differences.
Conclusion
By not requiring the dependent variable in the analysis to follow a specific distribution, the Wilcoxon Signed Rank Test offers a robust alternative for comparing means – or more accurately, medians – when dealing with non-normally distributed data or data on an ordinal scale. Its method of assessing median differences through signed ranks provides a more resilient approach to analyzing paired observations, making it an indispensable tool in the statistical analysis of dependent samples, particularly in fields where outliers or skewed distributions are common.
The Wilcox Sign Test in SPSS
Our research question for the Wilcoxon Sign Test is as follows:
Does the before-after measurement of the first and the last mid-term exam differ between the students who have been taught in a blended learning course and the students who were taught in a standard classroom setting?
We only measured the outcome of the mid-term exam on an ordinal scale (grade A to F); therefore a dependent samples t-test cannot be used. This is such because the distribution is only binominal and we do not assume that it approximates a normal distribution. Also both measurements are not independent from each other and therefore we cannot use the Mann-Whitney U-test.
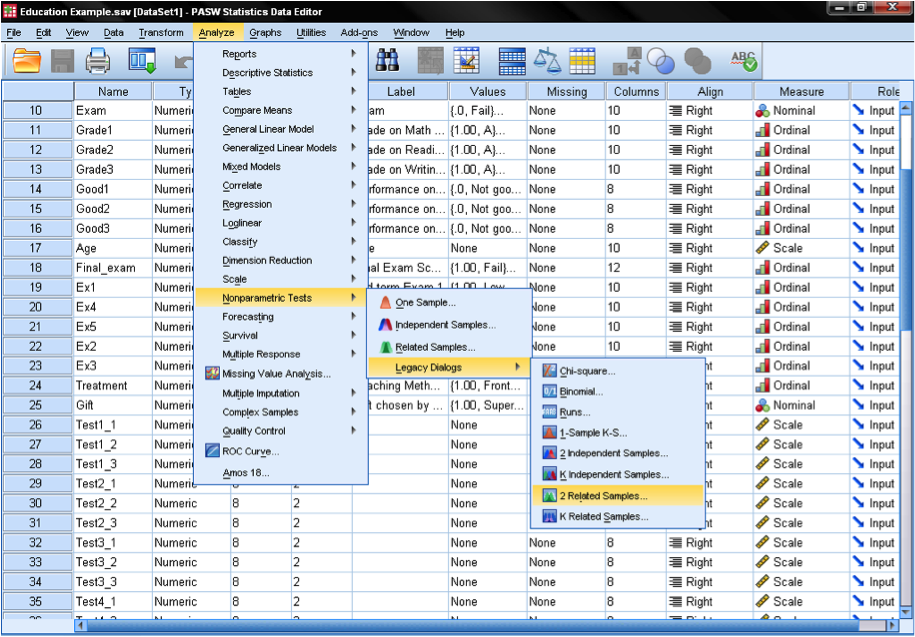
The Wilcoxon sign test can be found in Analyze/Nonparacontinuous-level Tests/Legacy Dialog/2 Related Samples…
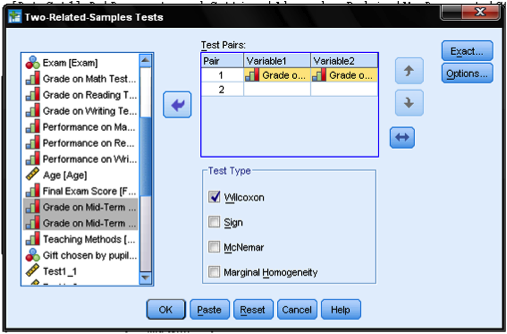
In the next dialog box for the nonparacontinuous-level two dependent samples tests we need to define the paired observations. We enter ‘Grade on Mid-Term Exam 1’ as variable 1 of the first pair and ‘Grade on Mid-Term Exam 2’ as Variable 2 of the first pair. We also need to select the Test Type. The Wilcoxon Signed Rank Test is marked by default. Alternatively we could choose Sign, McNamar, or Marginal Homogeneity.
Wilcoxon – The Wilcoxon signed rank test has the null hypothesis that both samples are from the same population. The Wilcoxon test creates a pooled ranking of all observed differences between the two dependent measurements. It uses the standard normal distributed z-value to test of significance.
Sign – The sign test has the null hypothesis that both samples are from the same population. The sign test compares the two dependent observations and counts the number of negative and positive differences. It uses the standard normal distributed z-value to test of significance.
McNemar – The McNemar test has the null hypothesis that differences in both samples are equal for both directions. The test uses dichotomous (binary) variables to test whether the observed differences in a 2×2 matrix including all 4 possible combinations differ significantly from the expected count. It uses a Chi-Square test of significance.
Marginal Homogeneity – The marginal homogeneity test has the null hypothesis that the differences in both samples are equal in both directions. The test is similar to the McNemar test, but it uses nominal variables with more than two levels. It tests whether the observed differences in a n*m matrix including all possible combinations differ significantly from the expected count. It uses a Chi-Square test of significance.
If the values in the sample are not already ranked, SPSS will sort the observations according to the test variable and assign ranks to each observation, correcting for tied observations. The dialog box Exact… allows us to specify an exact test of significance and the dialog box Options… defines how missing values are managed and if SPSS should output additional descriptive statistics.