Paired T-Test
The paired sample t-test, sometimes called the dependent sample t-test, is a statistical procedure used to determine whether the mean difference between two sets of observations is zero. In a paired sample t-test, each subject or entity is measured twice, resulting in pairs of observations. Common applications of the paired sample t-test include case-control studies or repeated-measures designs. Suppose you are interested in evaluating the effectiveness of a company training program. One approach you might consider would be to measure the performance of a sample of employees before and after completing the program, and analyze the differences using a paired sample t-test.
Hypotheses
Like many statistical procedures, the paired sample t-test has two competing hypotheses, the null hypothesis and the alternative hypothesis. The null hypothesis assumes that the true mean difference between the paired samples is zero. Under this model, all observable differences are explained by random variation. Conversely, the alternative hypothesis assumes that the true mean difference between the paired samples is not equal to zero. The alternative hypothesis can take one of several forms depending on the expected outcome. If the direction of the difference does not matter, a two-tailed hypothesis is used. Otherwise, an upper-tailed or lower-tailed hypothesis can be used to increase the power of the test. The null hypothesis remains the same for each type of alternative hypothesis. The paired sample t-test hypotheses are formally defined below:
• The null hypothesis (\(H_0\)) assumes that the true mean difference (\(\mu_d\)) is equal to zero.
• The two-tailed alternative hypothesis (\(H_1\)) assumes that \(\mu_d\) is not equal to zero.
• The upper-tailed alternative hypothesis (\(H_1\)) assumes that \(\mu_d\) is greater than zero.
• The lower-tailed alternative hypothesis (\(H_1\)) assumes that \(\mu_d\) is less than zero.
The mathematical representations of the null and alternative hypotheses are defined below:\(H_0:\ \mu_d\ =\ 0\)
Note. It is important to remember that hypotheses are never about data, they are about the processes which produce the data. In the formulas above, the value of \(\mu_d\) is unknown. The goal of hypothesis testing is to determine the hypothesis (null or alternative) with which the data are more consistent.
Need help with your research?
Schedule a time to speak with an expert using the calendar below.
User-friendly Software
Transform raw data to written interpreted APA results in seconds.
Assumptions
As a parametric procedure (a procedure which estimates unknown parameters), the paired sample t-test makes several assumptions. Although t-tests are quite robust, it is good practice to evaluate the degree of deviation from these assumptions in order to assess the quality of the results. In a paired sample t-test, the observations are defined as the differences between two sets of values, and each assumption refers to these differences, not the original data values. The paired sample t-test has four main assumptions:
- • The dependent variable must be continuous (interval/ratio).
- • The observations are independent of one another.
- • The dependent variable should be approximately normally distributed.
- • The dependent variable should not contain any outliers.
Level of Measurement
The paired sample t-test requires the sample data to be numeric and continuous, as it is based on the normal distribution. Continuous data can take on any value within a range (income, height, weight, etc.). The opposite of continuous data is discrete data, which can only take on a few values (Low, Medium, High, etc.). Occasionally, discrete data can be used to approximate a continuous scale, such as with Likert-type scales.
Independence
Independence of observations is usually not testable, but can be reasonably assumed if the data collection process was random without replacement. In our example, it is reasonable to assume that the participating employees are independent of one another.
Normality
To test the assumption of normality, a variety of methods are available, but the simplest is to inspect the data visually using a tool like a histogram (Figure 1). Real-world data are almost never perfectly normal, so this assumption can be considered reasonably met if the shape looks approximately symmetric and bell-shaped. The data in the example figure below is approximately normally distributed.
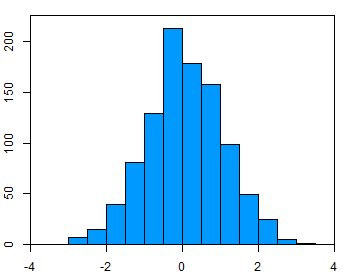
Outliers
Outliers are rare values that appear far away from the majority of the data. Outliers can bias the results and potentially lead to incorrect conclusions if not handled properly. One method for dealing with outliers is to simply remove them. However, removing data points can introduce other types of bias into the results, and potentially result in losing critical information. If outliers seem to have a lot of influence on the results, a nonparametric test such as the Wilcoxon Signed Rank Test may be appropriate to use instead. Outliers can be identified visually using a boxplot (Figure 2).
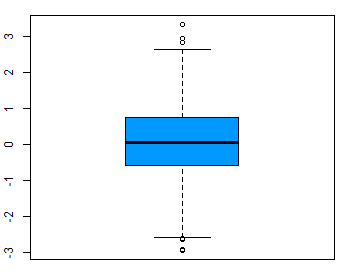
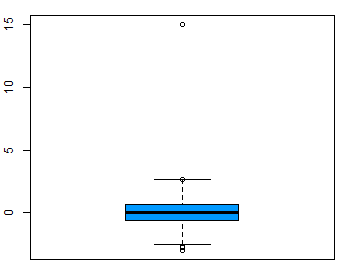
Procedure
The procedure for a paired sample t-test can be summed up in four steps. The symbols to be used are defined below:
- \(D\ =\ \)Differences between two paired samples
- \(d_i\ =\ \)The \(i^{th}\) observation in \(D\)
- \(n\ =\ \)The sample size
- \(\overline{d}\ =\ \)The sample mean of the differences
- \(\hat{\sigma}\ =\ \)The sample standard deviation of the differences
- \(T\ =\)The critical value of a t-distribution with (\(n\ -\ 1\)) degrees of freedom
- \(t\ =\ \)The t-statistic (t-test statistic) for a paired sample t-test
- \(p\ =\ \)The \(p\)-value (probability value) for the t-statistic.
The four steps are listed below:
- 1. Calculate the sample mean.
- \(\overline{d}\ =\ \cfrac{d_1\ +\ d_2\ +\ \cdots\ +\ d_n}{n}\)
- 2. Calculate the sample standard deviation.
- \(\hat{\sigma}\ =\ \sqrt{\cfrac{(d_1\ -\ \overline{d})^2\ +\ (d_2\ -\ \overline{d})^2\ +\ \cdots\ +\ (d_n\ -\ \overline{d})^2}{n\ -\ 1}}\)
- 3. Calculate the test statistic.
- \(t\ =\ \cfrac{\overline{d}\ -\ 0}{\hat{\sigma}/\sqrt{n}}\)
- 4. Calculate the probability of observing the test statistic under the null hypothesis. This value is obtained by comparing t to a t-distribution with (\(n\ -\ 1\)) degrees of freedom. This can be done by looking up the value in a table, such as those found in many statistical textbooks, or with statistical software for more accurate results.
- \(p\ =\ 2\ \cdot\ Pr(T\ >\ |t|)\) (two-tailed)
- \(p\ =\ Pr(T\ >\ t)\) (upper-tailed)
- \(p\ =\ Pr(T\ <\ t)\) (lower-tailed)
Determine whether the results provide sufficient evidence to reject the null hypothesis in favor of the alternative hypothesis.
Interpretation
There are two types of significance to consider when interpreting the results of a paired sample t-test, statistical significance and practical significance.
Statistical Significance
Statistical significance is determined by looking at the p-value. The p-value gives the probability of observing the test results under the null hypothesis. The lower the p-value, the lower the probability of obtaining a result like the one that was observed if the null hypothesis was true. Thus, a low p-value indicates decreased support for the null hypothesis. However, the possibility that the null hypothesis is true and that we simply obtained a very rare result can never be ruled out completely. The cutoff value for determining statistical significance is ultimately decided on by the researcher, but usually a value of .05 or less is chosen. This corresponds to a 5% (or less) chance of obtaining a result like the one that was observed if the null hypothesis was true.
Practical Significance
Practical significance depends on the subject matter. It is not uncommon, especially with large sample sizes, to observe a result that is statistically significant but not practically significant. In most cases, both types of significance are required in order to draw meaningful conclusions.
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
- *Edit your research questions and null/alternative hypotheses
* Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
*Justify your sample size/power analysis, provide references
*Explain your data analysis plan to you so you are comfortable and confident
*Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
*Clean and code dataset, and create composite scores
*Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
*Conduct analyses to examine each of your research questions
*Write-up results draft
*Provide APA 7th edition tables and figures
*Explain Chapter 4 findings
*Ongoing support for entire results chapter statistics
Please call 727-442-4290 to request a quote based on the specifics of your research, schedule using the calendar on this page, or email [email protected]