Conduct and Interpret a Mann-Whitney U-Test
What is the Mann-Whitney U-Test?
The Mann-Whitney U-test is a non-parametric method used to compare differences between two independent groups on a continuous or ordinal scale. It does not assume any specific distribution of the data, making it particularly useful for analyzing data that do not meet the normal distribution requirements of parametric tests like the t-test or ANOVA.
Essentially, the Mann-Whitney U-test evaluates whether the ranks of two independent samples differ significantly. This is achieved by ranking all the observations together, regardless of the group they belong to, and then summing the ranks for each group. The U statistic is calculated from these sums and used to assess the likelihood that the two samples come from the same population.
Unlike the t-test, which compares means, the Mann-Whitney U-test focuses on median differences, offering a robust alternative when data are not normally distributed or when dealing with ordinal data. It serves as the foundation for the Kruskal-Wallis H-test, which extends the comparison to more than two groups through multiple pairwise U-tests.
Developed initially by Wilcoxon in 1945 for equal sample sizes and expanded by Mann and Whitney in 1947 to accommodate unequal sample sizes, the Mann-Whitney U-test remains a cornerstone in statistical analysis for non-parametric data. Its flexibility and lack of stringent distributional assumptions make it a preferred choice for researchers dealing with non-normal data distributions or ordinal measurements.
Mann-Whitney help?
Option 1: User-friendly Software
Transform raw data to written interpreted APA results in seconds.
Option 2: Professional Statistician
Collaborate with a statistician to complete and understand your results.
The Mann-Whitney U-test utilizes a unified approach to ranking all observations across groups, distinguishing it from parametric counterparts like the t-test and F-test, which compare mean values. Its primary focus is on medians rather than means, enhancing its resilience against outliers and distributions with heavy tails. This non-parametric nature means it does not presuppose a specific distribution for the data, making it particularly suitable for data that are not normally distributed but are at least ordinal.
The robustness of the Mann-Whitney U-test stems from its ability to provide reliable comparisons without the strict distributional requirements needed for parametric tests. It’s ideal for evaluating median differences when dealing with non-normal distributions or ordinal data. For significance testing, the U-test assumes that with sample sizes greater than 80, or when each sample size exceeds 30, the distribution of the U statistic approximates a normal distribution. This allows the U statistic, derived from sample data, to be assessed against a normal distribution to determine confidence levels.
The essence of the Mann-Whitney U-test lies in its capacity to detect differences in medians that are influenced by an independent variable. It can also be interpreted as assessing whether one sample stochastically dominates another, with the U-value quantifying the frequency of observations from one group ranking higher than those from another. This is based on the probability concept that one sample is likely to yield higher values than the other. In some contexts, the Mann-Whitney U-test is also utilized to ascertain if two samples originate from the same population by comparing their distributions.
Other non-parametric tests for comparing distributions include the Kolmogorov-Smirnov Z-test and the Wilcoxon signed-rank test, each offering unique approaches to analyze data that does not fit the assumptions required by parametric methods.
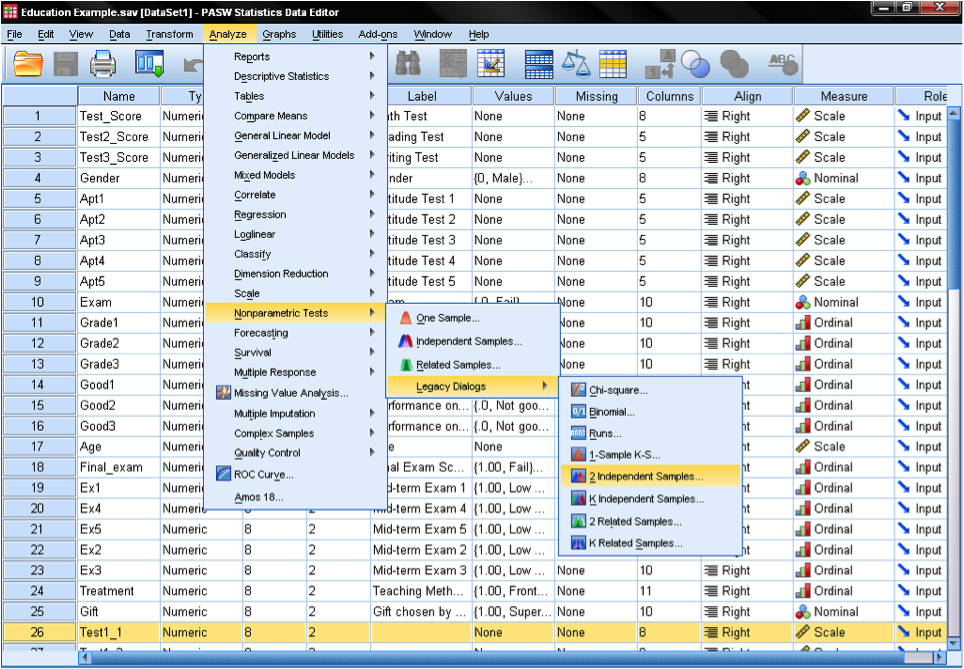
The Mann-Whitney U-Test in SPSS The research question for our U-Test is as follows: Do the students that passed the exam achieve a higher grade on the standardized reading test? The question indicates that the independent variable is whether the students have passed the final exam or failed the final exam, and the dependent variable is the grade achieved on the standardized reading test (A to F). The Mann-Whitney U-Test can be found in Analyze/Nonparacontinuous-level Tests/Legacy Dialogs/2 Independent Samples…
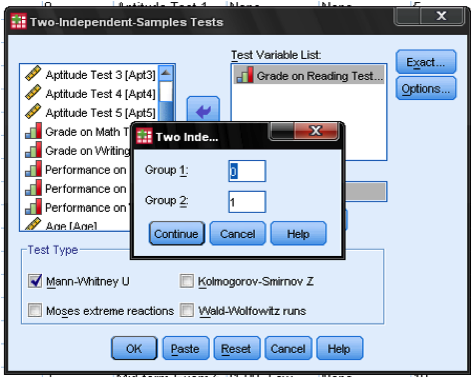
In the dialog box for the nonparacontinuous-level two independent samples test, we select the ordinal test variable ‘mid-term exam 1’, which contains the pooled ranks, and our nominal grouping variable ‘Exam‘. With a click on ‘Define Groups…‘ we need to specify the valid values for the grouping variable Exam, which in this case are 0 = fail and 1 = pass. We also need to select the Test Type. The Mann-Whitney U-Test is marked by default. Like the Mann-Whitney U-Test the Kolmogorov-Smirnov Z-Test and the Wald-Wolfowitz runs-test have the null hypothesis that both samples are from the same population. Moses extreme reactions test has a different null hypothesis: the range of both samples is the same. The U-test compares the ranking, Z-test compares the differences in distributions, Wald-Wolfowitz compares sequences in ranking, and Moses compares the ranges of the two samples. The Kolmogorov-Smirnov Z-Test requires continuous-level data (interval or ratio scale), the Mann-Whitney U-Test, Wald-Wolfowitz runs, and Moses extreme reactions require ordinal data. If we select Mann-Whitney U, SPSS will calculate the U-value and Wilcoxon’s W, which the sum of the ranks for the smaller sample. If the values in the sample are not already ranked, SPSS will sort the observations according to the test variable and assign ranks to each observation. The dialog box Exact… allows us to specify an exact non-paracontinuous-level test of significance and the dialog box Options… defines how missing values are managed and if SPSS should output additional descriptive statistics.