How to Conduct Multiple Linear Regression
Multiple Linear Regression Analysis involves more than just drawing a line through data points. It has three main steps: (1) examining the data’s correlation and direction, (2) fitting the line to the model, and (3) assessing the model’s validity and usefulness.
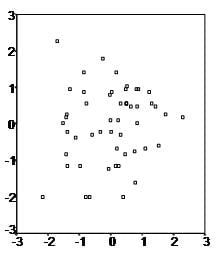
Start by analyzing scatter plots for each independent variable to check the data’s direction and correlation. For instance, the first scatter plot we show demonstrates a positive relationship between two variables.
The data is fit to run a multiple linear regression analysis.
Regression help?
Option 1: User-friendly Software
Transform raw data to written interpreted results in seconds.
Option 2: Professional Statistician
Collaborate with a statistician to complete and understand your results.
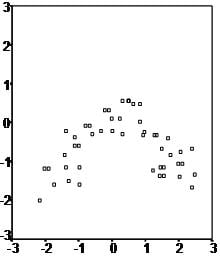
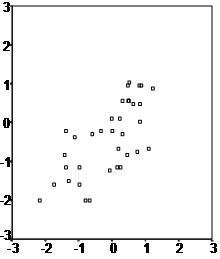
The second scatter plot seems to have an arch-shape this indicates that a regression line might not be the best way to explain the data, even if a correlation analysis establishes a positive link between the two variables. However, most often data contains quite a large amount of variability (just as in the third scatter plot example) in these cases it is up for decision how to best proceed with the data.
The second step of multiple linear regression is to formulate the model, i.e. that variable X1, X2, and X3 have a causal influence on variable Y and that their relationship is linear.
The third step of regression analysis is to fit the regression line.
Mathematically least square estimation is used to minimize the unexplained residual. The basic idea behind this concept is illustrated in the following graph.
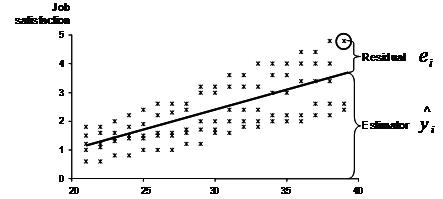
In our example we want to model the relationship between age, job experience, and tenure on one hand and job satisfaction on the other hand. The research team has gathered several observations of self-reported job satisfaction and experience, as well as age and tenure of the participant.
When we fit a line through the scatter plot (for simplicity only one dimension is shown here), the regression line represents the estimated job satisfaction for a given combination of the input factors. However in most cases the real observation might not fall exactly on the regression line.
Because we try to explain the scatter plot with a linear equation of
for i = 1…n. The deviation between the regression line and the single data point is variation that our model can not explain. This unexplained variation is also called the residual ei.
The method of least squares is used to minimize the residual.
The multiple linear regression’s variance is estimated by
where p is the number of independent variables and n the sample size.
The result of this equation could for instance be yi = 1 + 0.1 * xi1+ 0.3 * xi2 – 0.1 * xi3+ 1.52 * xi4. This means that for additional unit x1 (ceteris paribus) we would expect an increase of 0.1 in y, and for every additional unit x4 (c.p.) we expect 1.52 units of y.
Now that we got our multiple linear regression equation we evaluate the validity and usefulness of the equation.
The key measure to the validity of the estimated linear line is R². R² = total variance / explained variance. The following graph illustrates the key concepts to calculate R². In our example the R² is approximately 0.6, this means that 60% of the total variance is explained with the relationship between age and satisfaction.
As you can easily see the number of observations and of course the number of independent variables increases the R². However, over fitting occurs easily with multiple linear regression, over fitting happens at the point when the multiple linear regression model becomes inefficient. To identify whether the multiple linear regression model is fitted efficiently a corrected R² is calculated (it is sometimes called adjusted R²), which is defined
where J is the number of independent variables and N the sample size. As you can see the larger the sample size the smaller the effect of an additional independent variable in the model.
In our example R²c = 0.6 – 4(1-0.6)/95-4-1 = 0.6 – 1.6/90 = 0.582. Thus we find the multiple linear regression model quite well fitted with 4 independent variables and a sample size of 95.
The last step for the multiple linear regression analysis is the test of significance. Multiple linear regression uses two tests to test whether the found model and the estimated coefficients can be found in the general population the sample was drawn from. Firstly, the F-test tests the overall model. The null hypothesis is that the independent variables have no influence on the dependent variable. In other words the F-tests of the multiple linear regression tests whether the R²=0. Secondly, multiple t-tests analyze the significance of each individual coefficient and the intercept. The t-test has the null hypothesis that the coefficient/intercept is zero.
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
- Edit your research questions and null/alternative hypotheses
- Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
- Justify your sample size/power analysis, provide references
- Explain your data analysis plan to you so you are comfortable and confident
- Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
- Clean and code dataset
- Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
- Conduct analyses to examine each of your research questions
- Write-up results
- Provide APA 7th edition tables and figures
- Explain Chapter 4 findings
- Ongoing support for entire results chapter statistics
*Please call 877-437-8622 to request a quote based on the specifics of your research, or email [email protected].
Related Pages:
Multiple Linear Regression Video Tutorial