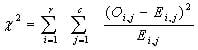Chi-Square Test of Independence
The Chi-Square test of independence is used to determine if there is a significant relationship between two nominal (categorical) variables. The frequency of each category for one nominal variable is compared across the categories of the second nominal variable. The data can be displayed in a contingency table where each row represents a category for one variable and each column represents a category for the other variable. For example, say a researcher wants to examine the relationship between gender (male vs. female) and empathy (high vs. low). The chi-square test of independence can be used to examine this relationship. The null hypothesis for this test is that there is no relationship between gender and empathy. The alternative hypothesis is that there is a relationship between gender and empathy (e.g. there are more high-empathy females than high-empathy males).
Calculate Chi Square Statistic by Hand
First we have to calculate the expected value of the two nominal variables. We can calculate the expected value of the two nominal variables by using this formula:
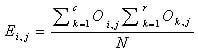
Where
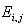 = expected value
= expected value
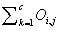
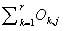
N = total number
After calculating the expected value, we will apply the following formula to calculate the value of the Chi-Square test of Independence:
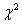
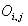
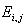
Degree of freedom is calculated by using the following formula:
DF = (r-1)(c-1)
Where
DF = Degree of freedom
r = number of rows
c = number of columns
Need assistance with your research?
Schedule a time to speak with an expert using the calendar below.
User-friendly Software
Transform raw data to written interpreted results in seconds.
Hypotheses
Null hypothesis: Assumes that there is no association between the two variables.
Alternative hypothesis: Assumes that there is an association between the two variables.
Hypothesis testing: Hypothesis testing for the chi-square test of independence as it is for other tests like ANOVA, where a test statistic is computed and compared to a critical value. The critical value for the chi-square statistic is determined by the level of significance (typically .05) and the degrees of freedom. The degrees of freedom for the chi-square are calculated using the following formula: df = (r-1)(c-1) where r is the number of rows and c is the number of columns. If the observed chi-square test statistic is greater than the critical value, the null hypothesis can be rejected.
Related Pages:
- Conduct and Interpret the Chi-Square Test of Independence
- Test of Independence: degrees of freedom
- Take the course: Chi Square Test of Independence
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
- Edit your research questions and null/alternative hypotheses
- Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
- Justify your sample size/power analysis, provide references
- Explain your data analysis plan to you so you are comfortable and confident
- Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
- Clean and code dataset
- Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
- Conduct analyses to examine each of your research questions
- Write-up results
- Provide APA 7th edition tables and figures
- Explain Chapter 4 findings
- Ongoing support for entire results chapter statistics
Please call 727-442-4290 to request a quote based on the specifics of your research, schedule using the calendar on this page, or email [email protected]