Chi-Square Goodness of Fit Test
Chi-Square goodness of fit test is a non-parametric test that is used to find out how the observed value of a given phenomena is significantly different from the expected value. In Chi-Square goodness of fit test, the term goodness of fit is used to compare the observed sample distribution with the expected probability distribution. Chi-Square goodness of fit test determines how well theoretical distribution (such as normal, binomial, or Poisson) fits the empirical distribution. In Chi-Square goodness of fit test, sample data is divided into intervals. Then the numbers of points that fall into the interval are compared, with the expected numbers of points in each interval.
Procedure for Chi-Square Goodness of Fit Test:
- Set up the hypothesis for Chi-Square goodness of fit test:
A. Null hypothesis: In Chi-Square goodness of fit test, the null hypothesis assumes that there is no significant difference between the observed and the expected value.
B. Alternative hypothesis: In Chi-Square goodness of fit test, the alternative hypothesis assumes that there is a significant difference between the observed and the expected value.
- Compute the value of Chi-Square goodness of fit test using the following formula:
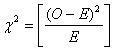 Where,
Where, - Degree of freedom: In Chi-Square goodness of fit test, the degree of freedom depends on the distribution of the sample. The following table shows the distribution and an associated degree of freedom:
| Type of distribution | No of constraints | Degree of freedom |
| Binominal distribution | 1 | n-1 |
| Poisson distribution | 2 | n-2 |
| Normal distribution | 3 | n-3 |
- Hypothesis testing: Hypothesis testing in Chi-Square goodness of fit test is the same as in other tests, like t-test, ANOVA, etc. The calculated value of Chi-Square goodness of fit test is compared with the table value. If the calculated value of Chi-Square goodness of fit test is greater than the table value, we will reject the null hypothesis and conclude that there is a significant difference between the observed and the expected frequency. If the calculated value of Chi-Square goodness of fit test is less than the table value, we will accept the null hypothesis and conclude that there is no significant difference between the observed and expected value.
Related Pages: