Should you use a one-tailed test or a two-tailed test for your data analysis?
When creating your data analysis plan or working on your results, you may have to decide if your statistical test should be a one-tailed test or a two-tailed test (also known as “directional” and “non-directional” tests respectively). So, what exactly is the difference between the two? First, it may be helpful to know what the term “tail” means in this context.
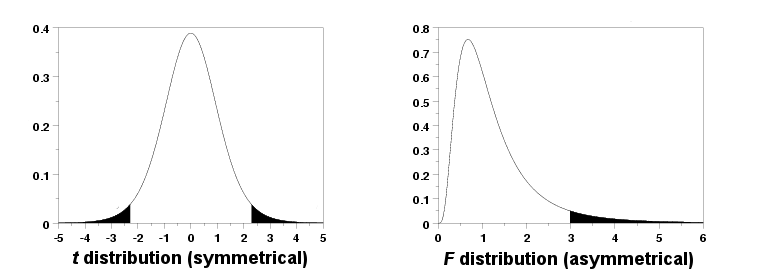
The tail refers to the end of the distribution of the test statistic for the particular analysis that you are conducting. For example, a t-test uses the t distribution, and an analysis of variance (ANOVA) uses the F distribution. The distribution of the test statistic can have one or two tails depending on its shape (see the figure below). The black-shaded areas of the distributions in the figure are the tails. Symmetrical distributions like the t and z distributions have two tails. Asymmetrical distributions like the F and chi-square distributions have only one tail. This means that analyses such as ANOVA and chi-square tests do not have a “one-tailed vs. two-tailed” option, because the distributions they are based on have only one tail.

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
But what if you are conducting a t-test, which has a two-tailed distribution? Now you will have to decide if a one-tailed or two-tailed test is most appropriate for your study. A two-tailed test is appropriate if you want to determine if there is any difference between the groups you are comparing. For instance, if you want to see if Group A scored higher or lower than Group B, then you would want to use a two-tailed test. This is because a two-tailed test uses both the positive and negative tails of the distribution. In other words, it tests for the possibility of positive or negative differences.
A one-tailed test is appropriate if you only want to determine if there is a difference between groups in a specific direction. So, if you are only interested in determining if Group A scored higher than Group B, and you are completely uninterested in possibility of Group A scoring lower than Group B, then you may want to use a one-tailed test. The main advantage of using a one-tailed test is that it has more statistical power than a two-tailed test at the same significance (alpha) level. In other words, your results are more likely to be significant for a one-tailed test if there truly is a difference between the groups in the direction that you have predicted. This is because only one tail of the distribution is used for the test.
So, which kind of test should you use? When in doubt, it is almost always more appropriate to use a two-tailed test. A one-tailed test is only justified if you have a specific prediction about the direction of the difference (e.g., Group A scoring higher than Group B), and you are completely uninterested in the possibility that the opposite outcome could be true (e.g., Group A scoring lower than Group B).
