Conduct and Interpret a Point-Biserial Correlation
What is Point-Biserial Correlation?
Like all correlation analyses the Point-Biserial Correlation measures the strength of association or co-occurrence between two variables. Correlation analyses express this strength of association in a single value, the correlation coefficient.
Point-Biserial Correlation Analysis in SPSS
Referring back to our initial example, we are interested in the strength of association between passing or failing the exam (variable exam) and the score achieved in the math, reading, and writing tests. In order to work correctly we need to correctly define the level of measurement for the variables in the variable view. There is no special command in SPSS to calculate the Point-Biserial Correlation Coefficient; SPSS needs to be told to calculate Pearson’s Bivariate Correlation Coefficient r with our data.
Since we use the Pearson r as Point-Biserial Correlation Coefficient, we should first test whether there is a relationship between both variables. As described in the section on Pearson’s Bivariate Correlation in SPSS, the first step is to draw the scatter diagram of both variables. For the Point-Biserial Correlation Coefficient this diagram would look like this.
Need help with your analysis?
Schedule a time to speak with an expert using the calendar below.
User-Friendly Software
Transform raw data into written, interpreted, APA formatted correlation results in seconds.
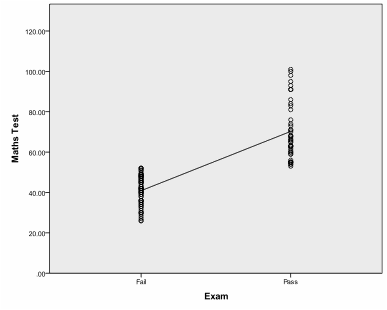
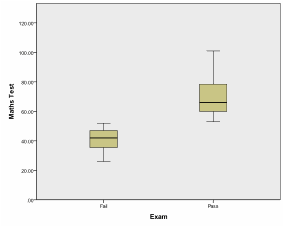
The diagram shows a positive slope and indicates a positive relationship between the math score and passing the final exam or failing it. Since our variable exam is measured on nominal level (0, 1), a better way to display the data is to draw a box plot. To create a box plot we select Graphs/Chart Builder… and select the Simple Box plot from the List in the Gallery. Drag Exam on the x-axis and Math Test on the y-axis.
A box plot displays the distribution information of a variable. More specifically it displays the quartiles of the data. The whiskers of the box span from the 0% quartile to the 100% quartile of the data. If the sample contains outliers they are displayed as data points outside the whiskers. The box spans from the 25% quartile to the 75% quartile and the median (the 50% quartile) is displayed as a strong line inside the box.
In our example we can see in the box plot that not only are the math scores higher on average for students who passed the final exam but also that there is almost no overlap between the two groups. Now that we have an understanding of the direction of our association between the two variables we can conduct the Point-Biserial Correlation Analysis.
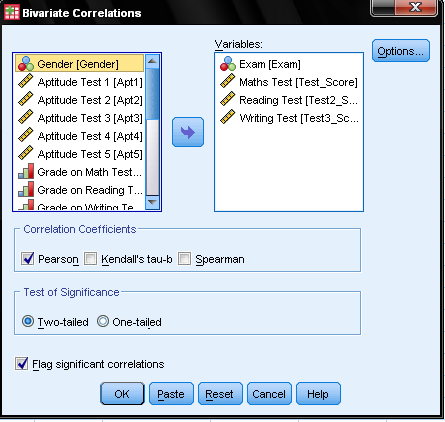
SPSS does not have a special procedure for the Point-Biserial Correlation Analysis. If a Point-Biserial Correlation is to be calculated in SPSS, the procedure for Pearson’s r has to be used. Therefore we open the Bivariate Correlations dialog Analyze/Correlate/Bivariate…
In the dialog box we add both variables to the list of variables to analyze and select Pearson Correlation Coefficient and two-tailed Test of Significance.
The Point-Biserial Correlation Coefficient is a correlation measure of the strength of association between a continuous-level variable (ratio or interval data) and a binary variable. Binary variables are variables of nominal scale with only two values. They are also called dichotomous variables or dummy variables in Regression Analysis. Binary variables are commonly used to express the existence of a certain characteristic (e.g., reacted or did not react in a chemistry sample) or the membership in a group of observed specimen (e.g., male or female). If needed for the analysis, binary variables can also be created artificially by grouping cases or recoding variables. However it is not advised to artificially create a binary variable from ordinal or continuous-level (ratio or scale) data because ordinal and continuous-level data contain more variance information than nominal data and thus make any correlation analysis more reliable. For ordinal data use the Spearman Correlation Coefficient rho, for continuous-level (ratio or scale) data use Pearson’s Bivariate Correlation Coefficient r. Binary variables are also called dummy. The Point-Biserial Correlation Coefficient is typically denoted as rpb .
Like all Correlation Coefficients (e.g. Pearson’s r, Spearman’s rho), the Point-Biserial Correlation Coefficient measures the strength of association of two variables in a single measure ranging from -1 to +1, where -1 indicates a perfect negative association, +1 indicates a perfect positive association and 0 indicates no association at all. All correlation coefficients are interdependency measures that do not express a causal relationship.
Mathematically, the Point-Biserial Correlation Coefficient is calculated just as the Pearson’s Bivariate Correlation Coefficient would be calculated, wherein the dichotomous variable of the two variables is either 0 or 1—which is why it is also called the binary variable. Since we use the same mathematical concept, we do need to fulfill the same assumptions, which are normal distribution of the continuous variable and homoscedasticity.
Typical questions to be answered with a Point-Biserial Correlation Analysis are as follows:
- Biology – Do fish react differently to red or green lighted stimulus as food signal? Is there an association between the color of the stimulus (red or green light) and the reaction time?
- Medicine – Does a cancer drug prolong life? How strong is the association between administering the drug (placebo, drug) and the length of survival after treatment?
- Sociology – Does gender have an influence on salary? Is there an association between gender (female, male) with the income earned?
- Social psychology – Is satisfaction with life higher the older you are? Is there an association between age group (elderly, not elderly) and satisfaction with life?
- Economics – Does analphabetism indicate a weaker economy? How strong is the association between literacy (literate vs. illiterate societies) and GDP?
Since all correlation analyses require the variables to be randomly independent, the Point-Biserial Correlation is not the best choice for analyzing data collected in experiments. For these cases a Linear Regression Analysis with Dummy Variables is the best choice. Also, many of the questions typically answered with a Point-Biserial Correlation Analysis can be answered with an independent sample t-Test or other dependency tests (e.g., Mann-Whitney-U, Kruskal-Wallis-H, and Chi-Square). Not only are some of these tests robust regarding the requirement of normally distributed variables, but also these tests analyze dependency or causal relationship between an independent variable and dependent variables in question.
Statistics Solutions can assist with your quantitative analysis by assisting you to develop your methodology and results chapters. The services that we offer include:
Edit your research questions and null/alternative hypotheses
Write your data analysis plan; specify specific statistics to address the research questions, the assumptions of the statistics, and justify why they are the appropriate statistics; provide references
Justify your sample size/power analysis, provide references
Explain your data analysis plan to you so you are comfortable and confident
Two hours of additional support with your statistician
Quantitative Results Section (Descriptive Statistics, Bivariate and Multivariate Analyses, Structural Equation Modeling, Path analysis, HLM, Cluster Analysis)
Clean and code dataset
Conduct descriptive statistics (i.e., mean, standard deviation, frequency and percent, as appropriate)
Conduct analyses to examine each of your research questions
Write-up results
Provide APA 6th edition tables and figures
Explain chapter 4 findings
Ongoing support for entire results chapter statistics
Please call 727-442-4290 to request a quote based on the specifics of your research, schedule using the calendar on this page, or email [email protected]