Conduct and Interpret a One-Way MANOVA
What is the One-Way MANOVA?
MANOVA is short for Multivariate ANalysis Of Variance. The main purpose of a one-way ANOVA is to test if two or more groups differ from each other significantly in one or more characteristics. A factorial ANOVA compares means across two or more variables. Again, a one-way ANOVA has one independent variable that splits the sample into two or more groups whereas the factorial ANOVA has two or more independent variables that split the sample in four or more groups. A MANOVA now has two or more independent variables and two or more dependent variables.
For some statisticians the MANOVA doesn’t only compare differences in mean scores between multiple groups but also assumes a cause effect relationship whereby one or more independent, controlled variables (the factors) cause the significant difference of one or more characteristics. The factors sort the data points into one of the groups causing the difference in the mean value of the groups.

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
Example:
A research team wants to test the user acceptance with a new online travel booking tool. The team conducts a study where they assign 30 randomly chosen people into 3 groups. The first group needs to book their travel through an automated online-portal; the second group books over the phone via a hotline; the third group sends a request via the online-portal and receives a call back. The team measures user acceptance as the behavioral intention to use the system, they do measure the latent construct behavioral intention with 3 variables – ease of use, perceived usefulness, effort to use.
| Independent Variables | |||
| Metric | Non-metric | ||
| DependentVariable | metric | Regression | ANOVA |
| Non-metric | Discriminant Analysis | χ² (Chi-Square) |
In the example, some statisticians argue that the MANOVA can only find the differences in the behavioral intention to use the system. However, some statisticians argue that you can establish a causal relationship between the channel they used and the behavioral intention for future use. It is generally assumed that the MANOVA is an ‘analysis of dependencies’. It is referred to as such because it proves an assumed cause-effect relationship between two or more independent variables and two or more dependent variables. In more statistical terms, it tests the effect of one or more independent variables on one or more dependent variables.
Other things you may want to try:
When faced with a question similar to the one in our example you could also try to run a 3 factorial ANOVAs, testing the influence of the three independent variables (the three channels) on each of the three dependent variables (ease of use, perceived usefulness, effort to use) individually. However running multiple factorial ANOVAs does not account for the full variability in all three dependent variables and thus the test has lesser power than the MANOVA.
Another thing you might want to try is running a factor analysis on the three dependent variables and then running a factorial ANOVA. The factor analysis reduces the variance within the three dependent variables to one factor, thus this procedure does have lesser power than the MANOVA.
A third approach would be to conduct a discriminant analysis and switch the dependent and independent variables. That is the discriminant analysis uses the three groups (online, phone, call back) as the dependent variable and identifies the significantly discriminating variables from the list of continuous-level variables (ease of use, perceived usefulness, effort to use).
Mathematically, the MANOVA is fully equivalent to the discriminant analysis. The difference consists of a switching of the independent and dependent variables. Both the MANOVA and the discriminant analysis are a series of canonical regressions. The MANOVA is therefore the best test use when conducting experiments with latent variables. This is due to the fact that it only requires a nominal scale for the independent variables which typically represent the treatment. This includes multiple continuous-level independent variables – which typically measure one latent (not directly observable) construct.
The MANOVA is much like the one-way ANOVA and the factorial ANOVA in that the one-way ANOVA has exactly one independent and one dependent variable. The factorial ANOVAs can have one or more independent variables but always has only one dependent variable. On the other hand the MANOVA can have two or more dependent variables.
| Independent Variables | |||
| 1 | 2+ | ||
| Dependent Variables | 1 | One-way ANOVA | Factorial ANOVA |
| 2+ | MANOVA | Factorial ANOVA |
The following table helps to quickly identify the right analysis of variance to choose in different scenarios.
Examples of typical questions that are answered by the MANOVA are as follows:
- Medicine – Does a drug work? Does the average life expectancy, perceived pain, and level of side-effects significantly differ between the three experimental groups that got the drug versus the established product, versus the control—and within each of the groups two subgroups for a high dose versus a low dose?
- Sociology – Are rich people living in the country side happier? Do they enjoy their lives more and have a more positive outlook on their futures? Do different income classes report a significantly different satisfaction, enjoyment and outlook on their lives? Does the area in which they live (suburbia/city/rural) affect their happiness and positive outlook?
- Management Studies – Which brands from the BCG matrix do have a higher customer loyalty, brand appeal, customer satisfaction? The BCG matrix measures brands in a brand portfolio with their business growth rate (high/low) and their market share (high/low). To which brand are customers more loyal, more attracted, and more satisfied with? Stars, cash cows, dogs, or question marks?
The One-Way MANOVA in SPSS
Our research question for the one-way MANOVA in SPSS is as follows:
Do gender and the outcome of the final exam influence the standardized test scores of math, reading, and writing?
The research question indicates that this analysis has multiple independent variables (exam and gender) and multiple dependent variables (math, reading, and writing test scores). We will skip the check for multivariate normality of the dependent variables; the sample we are going to look at has some violations of the assumption set forth by the MANOVA.
The MANOVA can be found in SPSS in Analyze/General Linear Model/Multivariate…, which opens the dialog for multivariate GLM procedure (that is GLM with more than one dependent variable). The multivariate GLM model is used to specify the MANOVAs.
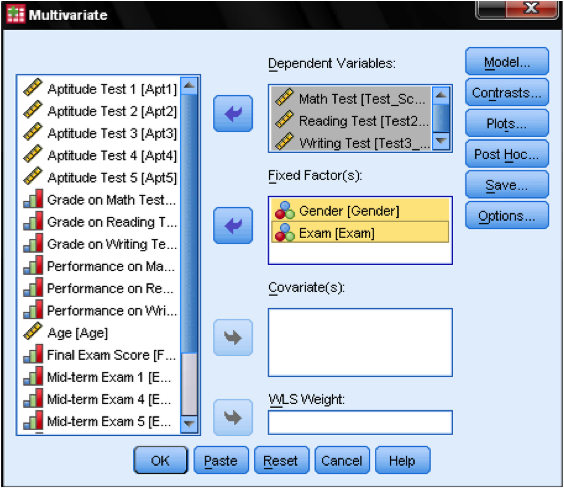
To answer our research question we need to specify a full-factorial model that includes the test scores for math, reading, and writing as dependent variable. Plus the independent variables gender and exam, which represent a fixed factor in our research design.
The dialog box Post Hoc tests is used to conduct a separate comparison between factor levels, this is useful if the MANOVA includes factors have more than two factor levels. In our case we select two factors and each has only two factor levels (male/female and pass/fail). The MANOVA’s F-test will test the null hypothesis that all means are the same. It does not indicate which of the means in our design are different. In order to find this information, post hoc tests need to be conducted as part of our MANOVA. In order to compare different groups (i.e., factor levels) we select the Student-Newman-Keuls test (or short S-N-K), which pools the groups that do not differ significantly from each other, thereby improving the reliability of the post hoc comparison by increasing the sample size used in the comparison. Additionally, it is simple to interpret.
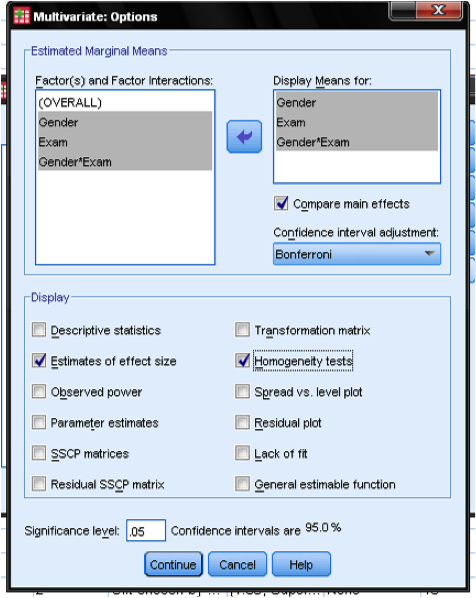
The Options… Dialog allows us to add descriptive statistics, the Levene Test and the practical significance to the output. Also we might want to add the pairwise t-tests to compare the marginal means of the main and interaction effects. The Bonferroni adjustment corrects the degrees of freedom to account for multiple pairwise tests.
The Contrast… dialog in the GLM procedure model gives us the option to group multiple groups into one and test the average mean of the two groups against our third group. Please note that the contrast is not always the mean of the pooled groups! Because Contrast = (mean first group + mean second group)/2. It is only equal to the pooled mean if the groups are of equal size. In our example we do without contrasts.
Lastly the Plots… dialog allows us to add profile plots for the main and interaction effects to our MANOVA. However it is easier to create the marginal means plots that are typically reported in academic journals in Excel.