Conduct and Interpret a One-Way MANCOVA
What is the One-Way MANCOVA?
MANCOVA is short for Multivariate Analysis of Covariance. The words “one” and “way” in the name indicate that the analysis includes only one independent variable. Like all analyses of covariance, the MANCOVA is a combination of a One-Way MANOVA preceded by a regression analysis.
In basic terms, the MANCOVA looks at the influence of one or more independent variables on one dependent variable while removing the effect of one or more covariate factors. To do that the One-Way MANCOVA first conducts a regression of the covariate variables on the dependent variable. Thus it eliminates the influence of the covariates from the analysis. Then the residuals (the unexplained variance in the regression model) are subject to an MANOVA, which tests whether the independent variable still influences the dependent variables after the influence of the covariate(s) has been removed. The One-Way MANCOVA includes one independent variable, one or more dependent variables and the MANCOVA can include more than one covariate, and SPSS handles up to ten. If the One-Way MANCOVA model has more than one covariate it is possible to run the MANCOVA with contrasts and post hoc tests just like the one-way ANCOVA or the ANOVA to identify the strength of the effect of each covariate.
The One-Way MANCOVA is most useful for two things: 1) explaining a MANOVA’s within-group variance, and 2) controlling confounding factors. Firstly, as explained in the section titled ‘How To Conduct a MANOVA,’ the analysis of variance splits the total variance of the dependent variable into:

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
- Variance explained by each of the independent variables (also called between-groups variance of the main effect)
- Variance explained by all of the independent variables together (also called the interaction effect)
- Unexplained variance (also called within-group variance)
The One-Way MANCOVA looks at the unexplained variance and tries to explain some of it with the covariate(s). Thus it increases the power of the MANOVA by explaining more variability in the model. [Note that just like in regression analysis and all linear model’s over-fitting might occur. That is, the more covariates you enter into the MANCOVA the more variance will be explained, but the fewer degrees of freedom the model has. Thus entering a weak covariate into the One-Way MANCOVA decreases the statistical power of the analysis instead of increasing it.]
Secondly, the One-Way MANCOVA eliminates the covariates’ effects on the relationship between independent variables and the dependent variables—an effect that is typically tested using a MANOVA. The concept is very similar to the concept behind partial correlation analysis; technically a MANCOVA is a semi-partial regression and correlation.
The One-Way MANCOVA needs at least four variables:
- One independent variable, which groups the cases into two or more groups, i.e., it has two or more factor levels. The independent variable has to be at least of nominal scale.
- Two or more dependent variables, which the independent variable influences. The dependent variables have to be of continuous-level scale (interval or ratio data). Also, they need to be homoscedastic and multivariate normal.
- One or more covariates, also called confounding factors or concomitant variables. These variables moderate the impact of the independent factor on the dependent variables. The covariates need to be continuous-level variables (interval or ratio data). The One-Way MANCOVA covariate is often a pre-test value or a baseline.
The One-Way MANCOVA in SPSS
The One-Way MANCOVA is part of the General Linear Models in SPSS. The GLM procedure in SPSS has the ability to include 1-10 covariates into an MANCOVA model. Without a covariate the GLM procedure calculates the same results as the MANOVA. The levels of measurement need to be defined upfront in order for the GLM procedure to work correctly.
Let us analyze the following research question:
Does the score achieved in the standardized math, reading, and writing test depend on the outcome of the final exam, when we control for the age of the student?
This research question means that the three test scores are the dependent variables, the outcome of the exam (fail vs. pass) is the independent variable and the age of the student is the covariate factor.
The One-Way MANCOVA can be found in Analyze/General Linear Model/Multivariate…
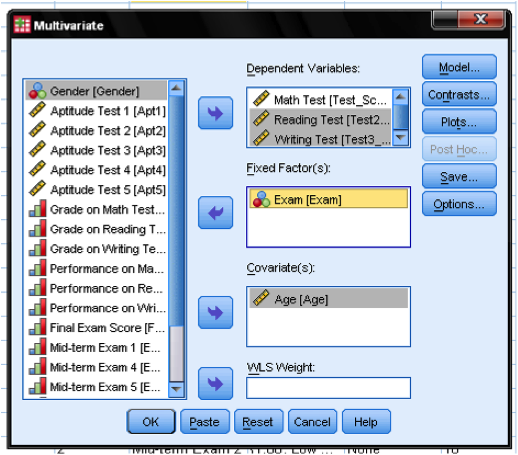
A click on this menu entry brings up the GLM dialog, which allows us to specify any linear model. For MANCOVA design we need to add the independent variable (exam) to the list of fixed factors. [Remember that the factor is fixed, if it is deliberately manipulated and not just randomly drawn from a population. In our MANCOVA example this is the case. This also makes the ANCOVA the model of choice when analyzing semi-partial correlations in an experiment, instead of the partial correlation analysis which requires random data.]
We need to specify a full-factorial model where the covariate is the students’ age, and the dependent variables are the math, reading, and writing test scores. In the dialog box Model… we leave all settings on the default. The default for all GLM (including the MANCOVA) is the full factorial model.
The field post hocs is disabled when one or more covariates are entered into the analysis. If we want to include a group comparison into our MANCOVA we would need to add contrasts to the analysis. If you wanted to compare all groups against a specific group you would need to select Simple as the Contrast Method, and also need to specify which group (the first or last) should be compared against all other groups.
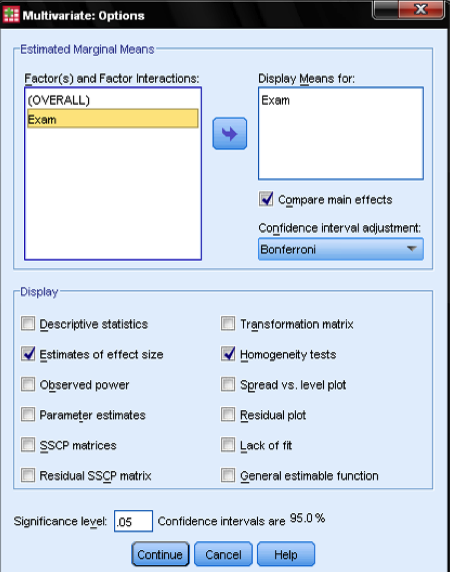
In the Options… dialog we can specify the additional statistics that SPSS is going to calculate. It is useful to include the marginal means for the factor levels and also to include the Levene test of homogeneity of error variances and the practical significance eta.
If the MANCOVA is a factorial MANCOVA and not a One-Way MANCOVA, i.e., includes more than one independent variable, you could choose to compare the main effects of those independent variables. The MANCOVA output would then include multiple ANOVAs that compare the factor levels of the independent variables. However, even if we adjust the confidence interval using the Bonferroni method, conducting multiple pairwise ANOVAs will multiply the error terms. Thus this method of testing main effects is typically not used anymore, and has been replaced by multivariate tests, e.g., Wilk’s’ Lambda.