McNemar, Marginal Homogeneity, Sign, Wilcoxon Tests
Non-parametric significance tests for two dependent samples are used when the researcher wants to study correlated, or matched, samples. This includes the before-after effect and matched paired studies: McNemar’s test, Test of Marginal Homogeneity, the Sign test, and Wilcoxon’s signed rank test. The McNemar test is the best test for dichotomous variables with two dependent sample studies. When a category of the sample is more than two, marginal homogeneity tests are appropriate; they are essentially an extension of the McNemar test for dependent samples. When the dependent variable samples are continuous in nature, then the sign and Wilcoxon tests are appropriate for two dependent sample studies.
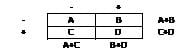
McNemar test: This test is also called the symmetry McNemar chi-square test. The McNemar test assesses if a statistically significant change in proportions have occurred on a dichotomous trait at two time points on the same population.
The McNemar test uses the chi-square distribution based on this formula:
Degrees-of-freedom = (rows – 1) (columns – 1) = 1
Interpreting significance from the McNemar test: If the computed value of McNemar test is less than the critical value using the degree of freedom, then it will not be significant. If the p value shown by the output is less than the desired significant level, then the difference between the two dependent samples will be statistically significant; otherwise, it will be non- significant.
Questions Answered:
Is there a change in the proportion of voters prior to and following the press conference?
The marginal homogeneity test: The marginal homogeneity test is much like the McNemar test, but in the marginal homogeneity test, the variables can take on more than two categories. This assesses the marginal frequencies of different rows and the corresponding columns. The marginal homogeneity test is interpreted like the McNemar test: if the p value is less than the desired significant value, then the dependent sample means will be different, and if the p value is greater than the desired level, then the mean of the dependent samples will be the same.
Questions Answered:
Is there a change in the proportion among raters’ agreement (low vs. medium vs. high) after the lecture?
The sign test: The sign test is used when dependent samples are ordered in pairs, where the bivariate random variables are mutually independent. The sign test converts the variable case into plus or minus signs (or ties, if applicable) and tests whether or not the plus sign differs from the minus sign. Based on the result, we can conclude if the two dependent sample means are the same or different. The measurement scaled is at least ordinal within each pair. The sign test is considered a weaker test, because it tests the pair value below or above the median and it does not measure the pair difference. The sign test is available in SPSS: click “menu,” select “analysis,” then click on “nonparametric,” and choose “two related sample” and “sign test.”
Interpreting the sign test: If the p value of the sign test is less than the desired value, then the two dependent sample means will be different (rejecting the null hypothesis). If the p value of the sign test is more than the desired significant level, then the two sample means will be considered the same (not rejecting the null hypothesis).
Questions Answered:
Which product of soda (Pepsi vs. Coke) is preferred among a group of 10 consumers?
The Wilcoxon signed-rank test: This test, also called the Wilcoxon matched-pairs signed ranks test, is used on continuous variables that are measured on two occasions and assessing if statistically significant differences exist on the score from time 1 to time 2. In SPSS, Wilcoxon signed-rank test is available by doing the following steps: in the menu click “analysis,” then select “nonparametric,” and choose “two related samples” and “Wilcoxon.” The SPSS output will also give information about the mean rank and the sum of ranks for the positive and negative sign. If the probability value is more than the desired value, than the Wilcoxon signed-rank test value will not be significant (not rejecting the null hypothesis). If that is the case, we can say that the median rank of the two dependent samples is the same. If the p value is less than the set significance value, then the median rank of the two dependent samples is the same (rejecting the null hypothesis)
Questions Answered:
Are IQ scores different from Kindergarten to 1st grade on the same group of 15 students?
Key terms and concepts
- Dependent sample: Two correlated samples, or a before and after study of a sample, are examples of the dependent sample. There are two types of dependency: (1) before after sample with the same people at different points of time and (2) matched paired study with the same people at different points of time.
- Type of significance estimate: Asymptotic, exact, or Monte-Carlo estimate methods are used to test the significance of the McNemar, marginal homogeneity, sign, and Wilcoxon tests.
- SPSS interface: These methods are available in SPSS, which can be accessed by selecting “analysis,” then “nonparametric,” and then the two related samples. Note that exact tests are available on “add on” module of SPSS.
Assumptions:
- Data distribution: McNemar, Marginal Homogeneity, Sign, and Wilcoxon Signed RankTests are non–parametric (distribution free) tests, so we do not assume that the data is normally distributed.
- Two sample: Data should be from two samples. The population may differ for the two samples.
- Dependent sample: Dependent samples should be a paired sample or matched. Also known as ‘before–after’ sample.
- Adequate sample size: For the McNemar test, the number of the case should be equal to the a-d diagonal. If we are using the binomial test, then it should be equal to a+d diagonal.
Need More Help?
Check out our online course for conducting a McNemar Test here.
Related Pages: