Understanding the Wilcoxon Signed Rank Test
The Wilcoxon signed rank test is the non-parametric counterpart to the dependent samples t-test. It is designed for situations where the t-test assumptions, particularly regarding metric and normally distributed data, are not met. This test is especially useful for ranked or ordinal data. It provides an excellent alternative for analyzing repeated measures or paired observations without requiring a normal distribution.
Key Features of the Wilcoxon Signed Rank Test
- Non-parametric Nature: The test suits ordinal data or non-normally distributed data.
- W-Statistic: The test calculates the W-statistic, which approximates a normal distribution for samples larger than 10 paired observations.
Application Scenario: Evaluating a New Teaching Method
A research team aims to assess the effectiveness of a novel teaching method on improving children’s literacy levels. They study 20 children, measuring literacy on a 0 to 10 scale before and after implementing the teaching method. The pre-intervention average literacy score stands at 5.9, which then rises to 7.6 post-intervention.
Given the data’s nature and its non-normal distribution, we identify the Wilcoxon signed rank test as the most appropriate statistical method for this analysis. The paired nature of the measurements (pre- and post-intervention scores) makes independent tests like the Mann-Whitney U-test unsuitable.
Conducting the Wilcoxon Signed Rank Test: Step-by-Step
Rank the Differences: Compute the differences between paired observations and rank their absolute values, ignoring the sign.
Assign Signs to Ranks: Reintroduce the signs (positive or negative) to the ranks based on the direction of the difference (whether the post-score was higher or lower than the pre-score).
Calculate the W-Statistic: Sum the ranks for positive differences and for negative differences separately. The W-statistic uses the smaller of the two sums to assess the significance of the observed differences.
Interpret the Results: Using the calculated W-statistic, determine whether the literacy scores have significantly changed post-intervention, based on a predefined significance level (e.g., α = 0.05).
Conclusion
The Wilcoxon signed rank test offers a robust alternative to the dependent samples t-test when the data do not meet its assumptions. It allows researchers to analyze changes in ordinal data or non-normally distributed metric data from repeated measures or paired observations. By applying this test, the research team can determine if the new teaching method has a statistically significant effect on children’s literacy levels. This provides valuable insights into its efficacy.
The first step of the Wilcoxon signed rank test is to calculate the differences between repeated measurements. Next, researchers calculate the absolute differences..
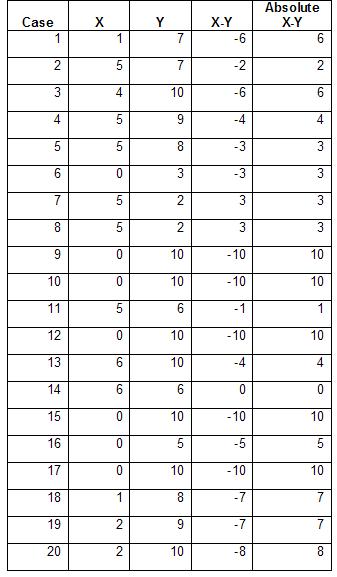
The next step of the Wilcoxon sign test is to sign each rank. If the original difference < 0 then the rank is multiplied by -1; if the difference is positive the rank stays positive.
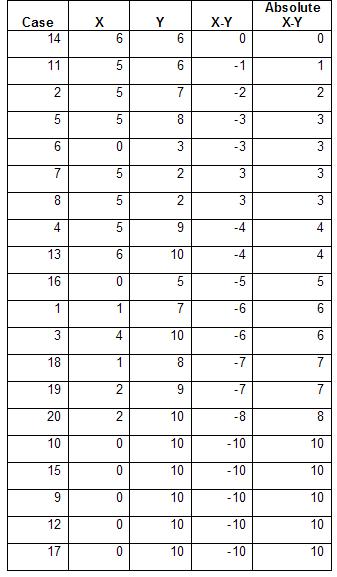
For the Wilcoxon signed rank test we can ignore cases where the difference is zero. For all other cases we assign their relative rank. In case of tied ranks, we calculate the average rank. For example, if rank 10 and 11 have the same observed differences, we assign both rank 10.5.
The next step of the Wilcoxon sign test is to sign each rank. If the original difference < 0 then the rank is multiplied by -1; if the difference is positive the rank stays positive.
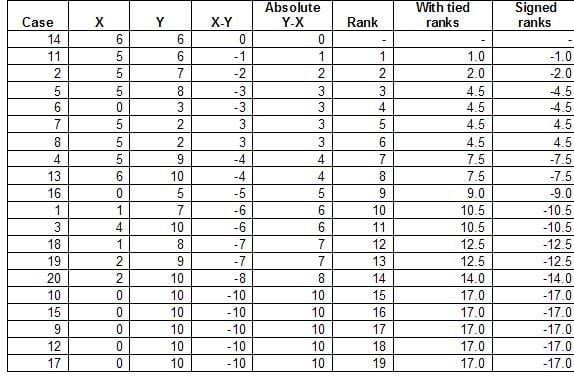
The next step is to calculate the W+ and W-.
W+ = 4.5 + 4.5 = 9
W- = 1+ 2 + 4.5 + 4.5 + 7.5 + 7.5 + 9 + 10.5 + 10.5 + 12.5 + 12.5 + 14 + 17+ 17 + 17 + 17 + 17 = 181
We can double check this knowing 
Therefore, 
and 
For large samples with n>10 the W-statistics approximates normal distribution, with 
Further, we must make a compensation for ties, 4, 2, 2, 2, and 5, so we must reduce the variance by 
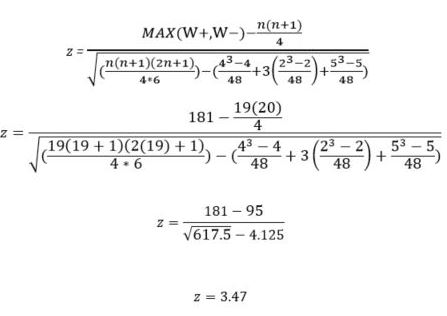
The shortcut to the hypothesis testing of the Wilcoxon signed rank-test is knowing the critical z-value for a 95% confidence interval (or a 5% level of significance) which is z = 1.96 for a two-tailed test and directionality. Whenever a test is based the normal distribution the sample z value needs to be 1.96 or higher to reject the null hypothesis.
Take the Course: Wilcoxon Signed Rank Test
If you’re like others, you’ve invested a lot of time and money developing your dissertation or project research. Finish strong by learning how our dissertation specialists support your efforts to cross the finish line.