Conduct and Interpret a Dependent Sample T-Test
What is the Dependent Sample T-Test?
The dependent sample t-test is a member of the t-test family. All tests from the t-test family compare one or more mean scores with each other. The t-test family is based on the t-distribution, sometimes also called Student’s t. Student is the pseudonym used by W. S. Gosset in 1908 to publish the t-distribution based on his empirical findings on the height and the length of the left middle finger of criminals in a local prison.
Within the t-test family the dependent sample t-test compares the mean scores of one group in different measurements. It is also called the paired t-test, because measurements from one group must be paired with measurements from the other group. The dependent sample t-test is used when the observations or cases in one sample are linked with the cases in the other sample. This is typically the case when repeated measures are taken, or when analyzing similar units or comparable specimen.

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
Making repeated measurements or pairing observations is very common when conducting experiments or making observations with time lags. Pairing the measured data points is typically done in order to exclude any cofounding or hidden factors (cf. partial correlation). It is also often used to account for individual differences in the baselines, for example pre-existing conditions in clinical research. Consider the example of a drug trial where the participants have individual differences that might have an impact on the outcome of the trial. The typical drug trial splits all participants into a control and the treatment group. The dependent sample t-test can correct for the individual differences or baselines by pairing comparable participants from the treatment and control group. Typical grouping variables are easily obtainable statistics such as age, weight, height, blood pressure. Thus the dependent-sample t-test analyzes the effect of the drug while excluding the influence of different baseline levels of health when the trial began.
Pairing data points and conducting the dependent sample t-test is a common approach to establish causality in a chain of effects. However, the dependent sample t-test only signifies the difference between two mean scores and a direction of change—it does not automatically give a directionality of cause and effect.
Since the pairing is explicitly defined and thus new information added to the data, paired data can always be analyzed with the independent sample t-test as well, but not vice versa. A typical guideline to determine whether the dependent sample t-test is the right test is to answer the following three questions:
- Is there a direct relationship between each pair of observations (e.g., before vs. after scores on the same subject)?
- Are the observations of the data points definitely not random (e.g., they must not be randomly selected specimen of the same population)?
- Do both samples have to have the same number of data points?
If the answer is yes to all three of these questions the dependent sample t-test is the right test, otherwise use the independent sample t-test. In statistical terms the dependent samples t-test requires that the within-group variation, which is a source of measurement errors, can be identified and excluded from the analysis.
The Dependent Sample T-Test in SPSS
Our research question for the dependent sample t-test is as follows:
Do students aptitude test1 scores differ from their aptitude test2 scores?
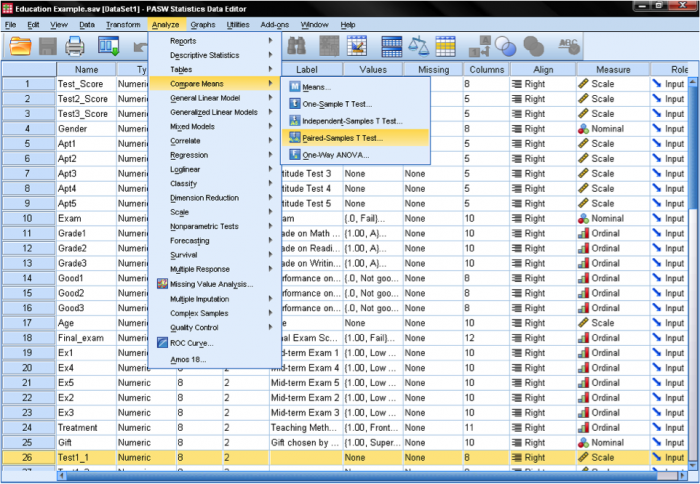
The dependent samples t-test is found in Analyze/Compare Means/Paired Samples T Test…
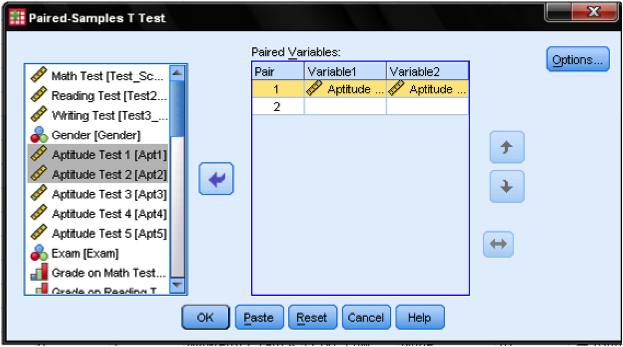
We need to specify the paired variable in the dialog box for the dependent samples t-test. We need to inform SPSS what is the before and after measurement. SPSS automatically assumes that the second dimension of the pairing is the case number, i.e. that case number 1 is a pair of measurements between variable 1 and 2.
Although we could specify multiple dependent samples t-test that are executed at the same time, our example only looks at the first and the second aptitude test. Thus we drag & drop ‘Aptitude Test 1‘ into the cell of pair 1 and variable 1, and ‘Aptitude Test 2’ into the cell pair 1 and variable 2. The Options… button allows to define the width of the control interval and how missing values are managed. We leave all settings as they are.