Conduct and Interpret a Profile Analysis
What is the Profile Analysis?
Profile Analysis is mainly concerned with test scores, more specifically with profiles of test scores. Why is that relevant? Tests are commonly administered in medicine, psychology, and education studies to rank participants of a study. A profile shows differences in scores on the test. If a psychologist administers a personality test (e.g., NEO), the respondent gets a test profile in return showing the scores on the Neuroticism, Extraversion, Agreeableness, Consciousness, and Openness dimensions. Similarly, many tests such as GMAT, GRE, SAT, and various intelligence questionnaires report profiles for abilities in reading, writing, calculating, and critically reasoning.
Typically test scores are used to predict behavioral items. In education studies it is common to predict test performance, for example using the SAT to predict the college GPA when graduating. Cluster analysis and Q-test have been widely used to build predictive models for this purpose.
What is the purpose of Profile Analysis?
Profile Analysis helps researchers to identify whether two or more groups of test takers show up as a significantly distinct profile. It helps to analyze patterns of tests, subtests, or scores. The analysis may be across groups or across scores for one individual.

Discover How We Assist to Edit Your Dissertation Chapters
Aligning theoretical framework, gathering articles, synthesizing gaps, articulating a clear methodology and data plan, and writing about the theoretical and practical implications of your research are part of our comprehensive dissertation editing services.
- Bring dissertation editing expertise to chapters 1-5 in timely manner.
- Track all changes, then work with you to bring about scholarly writing.
- Ongoing support to address committee feedback, reducing revisions.
What does that mean?
The profile analysis looks at profile graphs. A profile graph is simply the mean score of the one group of test takers with the other group of test takers along all items in the battery. The main purpose of the profile analysis is to identify how good a test is. Typically the tests consist of multiple item measurements and are administered over a series of time points. You could use a simple ANOVA to compare the test items, but this violates the independence assumption in two very important ways. Firstly, the scores on each item are not independent – item batteries are deliberately designed to have a high correlation among each other. Secondly, if you design a test to predict group membership (e.g., depressed vs. not depressed, likely to succeed vs. not like to succeed in college), you want the item battery to best predict the outcome. Thus item battery and group membership are also not independent.
What is the solution to this problem?
Since neither the single measurements on the items nor the group membership are independent, they needed to be treated as a paired sample. Statistically the Profile Analysis is similar to a repeated measures ANOVA.
Example:
A research team wants to create a new test for a form of cancer that seems to present in patients with a very specific history and diet. The researchers collect data on ten questions from patients that present with the cancer and a randomly drawn sample of people who do not present with the cancer.
Profile Analysis is now used to check whether the ten questions significantly differentiate between the groups that presents with the illness and the group that does not. Profile analysis takes into account that neither items among each other nor subject assignment to groups is random.
Profile Analysis is also a great way to understand and explore complex data. The results of the profile analysis help to identify and focus on the relevant differences and help the researcher to select the right contrasts, post hoc analysis, and statistical tests when a simple ANOVA or t-test would not suffice. However profile analysis has its limitations, especially when it comes to standard error of measurement and predicting a single person’s score.
Alternatives to the Profile Analysis are the Multidimensional Scaling, and Q-Analysis. In Q-Analysis the scores of an individual on the item battery are treated as an independent block (just as in Profile Analysis). The Q-Analysis then conducts a rotated factor analysis on these blocks, extracting relevant factors and flagging the items that define a factor.
Another alternative to Profile Analysis is a two-way MANOVA (or doubly MANOVA). In this design the repeated measures would enter the model as the second dependent variable and thus the model elegantly circumvents the sphericity assumption.
The Profile Analysis in SPSS
The research question we will examine for the Profile Analysis is as follows:
Do the students who passed the final exam and the students who failed the final exam have a significantly different ranking in their math, reading, and writing test?
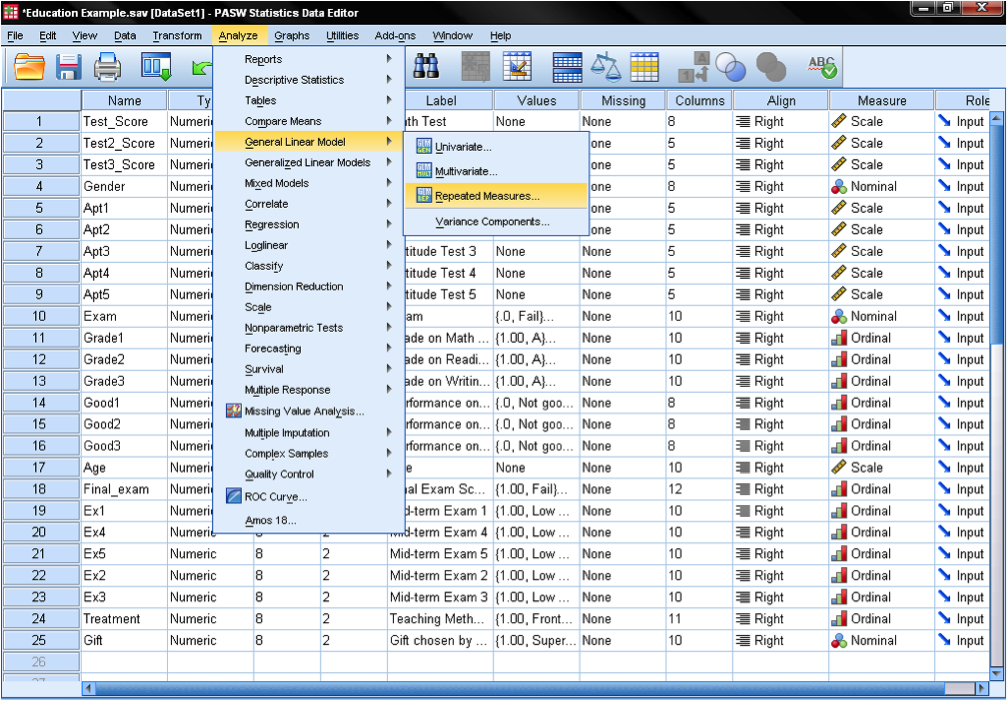
The Profile Analysis uses the repeated measures GLM module of SPSS, like the repeated measures ANOVA and ANCOVA. The Profile Analysis can be found in SPSS in the menu Analyze/General Linear Model/Repeated Measures…
The dialog box that opens is different than the GLM module for independent measures. Before specifying the model we need to group the repeated measures—the item battery we want to test. In our example we want to test if the standardized test, which consists of three items (math, reading, writing), correctly classifies the two groups of students that either pass or fail the final exam.
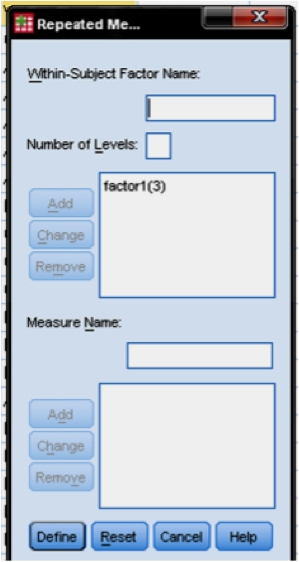
This is done by creating a within-subject factor. The item battery is called the within-subject factor of our Profile Analysis, because it represents the different observations of one subject. Our item battery contains three items – one score for math, one for reading, and one for writing. Thus we create and add a factor labeled factor1 with three factor levels.
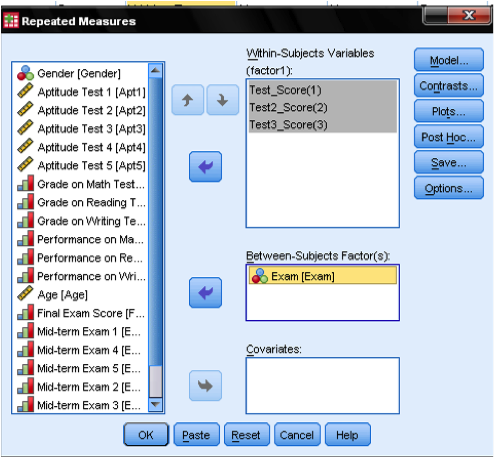
The next dialog box allows us to specify the Profile Analysis. First we need to add the three test items to the list of within-subjects variables. We then add the exam variable to the list of between-subjects factors. We can leave all other settings on default, apart from the plots.
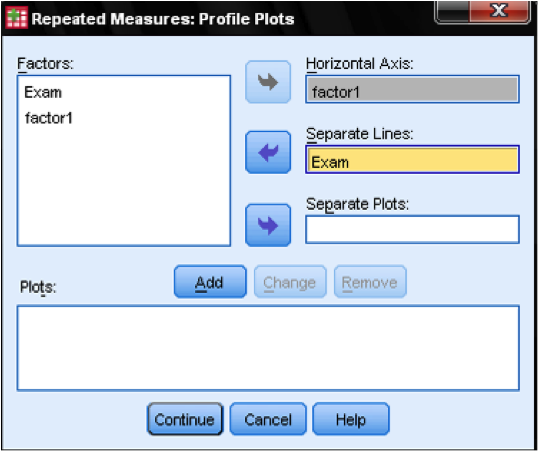
To create the profile plots we want the items (or subtests) on the horizontal axis with the groups as separate lines. We also need the Levene test for homoscedasticity to check the assumptions of the Profile Analysis, the Levene Test can be included in the dialog Options…